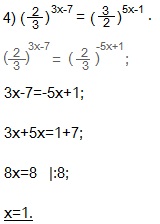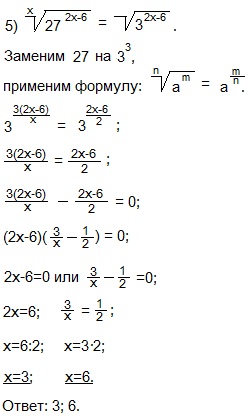Решение простейших показательных уравнений

Решение показательных уравнений — это материал 10-11 класса. Какие же уравнения называются показательными?

Уравнения, содержащие переменную в показателе степени, называются показательными уравнениями.

Простейшие показательные уравнения

Простейшие показательные уравнения — это уравнения вида: a^x=a^y. Отсюда следует равенство: х=у. В самом деле, степени с одинаковыми основаниями могут быть равными только в том случае, если равны показатели этих степеней.

Ниже вы найдете примеры решения показательных уравнений.

Уравнение 1

Решить уравнение:

 5^x=125.  Представим число 125 в виде степени числа 5:

5^x=5³; Степени равны, их основания равны, значит, и показатели степеней будут равны:

x=3.

Уравнение 2

 4^x=32. Представим левую и правую части в виде степеней с основанием 2:

(2²)^x=2⁵; используем формулу возведения степени в степень: (a^x)^y=a^xy  

2^2x=2⁵;

2x=5  |:2

x=2,5.

Уравнение 3

 3^2x-1=81. Число 81 представим в виде степени числа 3:

3^2x-1=3⁴;  приравняем показатели степеней с одинаковыми основаниями:

2x-1=4;  решаем простейшее линейное уравнение:

2x=4+1;

2x=5  |:2;

x=2,5.

Уравнение 4

 

К правой части применяем формулу: (a/b)^-x=(b/a)^x. Получим равенство степеней с одинаковыми основаниями.

Приравниваем показатели степеней и находим х из полученного линейного уравнения.

Уравнение 5

 

 

 

Приравняем показатели степеней с одинаковыми основаниями.

Переносим степень из правой части уравнения в левую.

Вынесли общий множитель (2х-6) за скобки. Произведение двух или нескольких множителей равно нулю, если один из множителей равен нулю, а другие при этом значении не теряют смысла. Содержимое каждой из скобок приравниваем к нулю и решаем простейшие уравнения.

Уравнение 6

7∙5^x-5^x+1=2∙5³.

Показатели степеней складываются, если степени перемножаются ( a^x∙a^y=a^x+y ), поэтому:

7∙5^x-5^x∙5¹=2∙5³;

5^x(7-5)=2∙5³;  вынесли общий множитель за скобки.

5^x∙2=2∙5³     |:2

5^x=5³;  отсюда следует:

x=3.

Уравнение 7

 3^x+2+4∙3^x+1=21.  Применим формулу: a^x+y=a^x∙a^y  (При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают):

3^x∙3²+4∙3^x∙3¹=21; вынесем общий множитель за скобки:

3^x(9+12)=21;

3^x∙21=21  |:21

3^x=1; число 1 можно представлять в виде нулевой степени с любым основанием.

3^x=3⁰;

x=0.

Уравнение 8

5^1+2x+5^2x+3=650.  Решаем аналогично.

5¹∙5^2x+5^2x∙5³=650;

5^2x(5+125)=650;

5^2x∙130=650   |:130

5^2x=5; приравняем показатели равных степеней с основаниями 5.

2x=1  |:2

x=0,5.

Методы решения показательных уравнений достаточно известны и мы подробно объяснили, как их применять при решении показательных уравнений на примерах.