Выведем уравнение касательной к графику функции y=f (x) в точке с абсциссой х0. Для наглядности используем график из 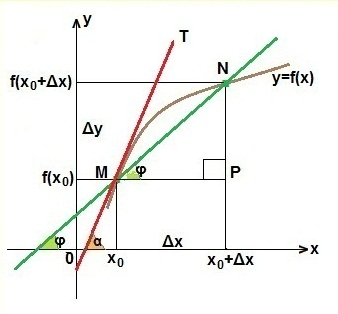 предыдущего урока 10.3. («Определение производной. Геометрический смысл производной») и выведем уравнение касательной МТ.
предыдущего урока 10.3. («Определение производной. Геометрический смысл производной») и выведем уравнение касательной МТ.
Так как точку М мы взяли произвольно, то должны получить уравнение касательной, которое будет справедливо для любой функции y=f (x), имеющей касательную в определенной точке с абсциссой х0.
Итак, любую прямую можно записать в виде y=kx+b, где k — угловой коэффициент прямой. Мы теперь знаем, что в качестве углового коэффициента можно взять f '(х0) — значение производной функции y=f (x) в точке с абсциссой х0. Эта точка является общей точкой для функции и для касательной МТ.
Таким образом, касательная МТ имеет вид: y=f '(х0)·x+b. Осталось определить значение b. Это мы сделаем просто: подставим координаты точки М в последнее равенство, т.е. вместо х запишем х0, а вместо у подставим f (х0). Получаем равенство:
f (х0) =f '(х0)·х0+b.
Отсюда b=f (х0) - f '(х0)·х0. Подставляем это значение b в равенство: y=f '(х0)·x+b. Тогда:
y =f '(х0)·х+f (х0) - f '(х0)·х0. Упростим.
y=f (х0)+(f '(х0)·х - f '(х0)·х0) или
y=f (х0)+f '(х0)(х - х0). Это и есть искомое уравнение касательной МТ.
Смотрите видео 10.3.1. Уравнение касательной.
Выполнить следующие задания
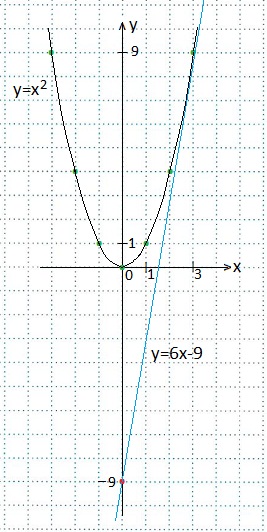
1. Написать уравнение касательной к графику функции y=x2 в точке x0=3. Сделать чертеж.
Решение.
 Запишем уравнение касательной к графику функции y=f (x) в точке с абсциссой x0 в общем виде:
Запишем уравнение касательной к графику функции y=f (x) в точке с абсциссой x0 в общем виде:
y=f (x0) +f '(x0)(x-x0).
Находим значение данной функции в точке с данной абсциссой:
f (x0)=f (3)=32=9.
Находим производную f '(x)=(x2)'=2x и находим значение этой производной при х=3.
Тогда f '(x0)=f '(3)=2·3=6.
Подставим найденные значения
f (x0)=9 и f '(x0)=6 в уравнение касательной, получим:
y=9+6·(x-3);
y=9+6x-18;
y=6x-9 — искомое уравнение касательной.
Ответ: y=6x-9.
2. Написать уравнение касательной к графику функции
Решение.
Записываем общее уравнение касательной: y=f (x0) +f '(x0)(x-x0). Находим значение данной функции в точке х=1, получаем:
f (x0)=f (1) = 1. Найдем производную данной функции по формуле производной степени:
f '(x)=(x-2)=-2x-2-1=-2x-3.
Находим значение этой производной при х=1.
f '(x0)=f (1)=-2·(1)-3 =-2. Подставляем найденные значения в общее уравнение касательной:
y=1-2(x-1);
y=1-2x+2;
y=-2x+3 - искомое уравнение касательной.
Ответ: y=-2x+3.


Класс