Формулы приведения в тригонометрии тригонометрических функций

Формулы приведения относятся к тригонометрической функции, которая использует периодичность для преобразования тригонометрической функции с относительно большим углом в тригонометрическую функцию с относительно небольшим углом.

Содержание

Формулы взаимосвязи между углами противоположными на 360 градусов или круг

Эти формулы устанавливают связь между углами противоположными на 360 градусов или круг. Значение одной и той же тригонометрической функции для того же угла на противоположной стороне равно.

Пусть α — любой острый угол, выражение угла в радианной системе:

$cos(2k \pi+\alpha)=cos \alpha$ $(k \in Z)$

$sin(2k \pi+\alpha)=sin \alpha$ $(k \in Z)$

$tg(2k \pi+\alpha)=tg \alpha$ $(k \in Z)$

$ctg(2k \pi+\alpha)=ctg \alpha$ $(k \in Z)$

В градусной мере тригонометрическая функция угла будет выражаться формулами:

$sin(\alpha+k \cdot 360^0)=sin \alpha$ $(k \in Z)$ .

$cos(\alpha+k \cdot 360^0)=cos \alpha$ $(k \in Z)$ .

$tg(\alpha+k \cdot 360^0)=tg \alpha$ $(k \in Z)$ .

$ctg(\alpha+k \cdot 360^0)=ctg \alpha$ $(k \in Z)$ .

$sec(\alpha+k \cdot 360^0)=sec \alpha$ $(k \in Z)$ .

$cosec(\alpha+k \cdot 360^0)=cosec \alpha$ $(k \in Z)$ .

Формулы тригонометрической функции π + α, связанные с значением тригонометрической функции α

Эта группа устанавливает связь между значением тригонометрической функции π + α и значением тригонометрической функции α.

Пусть α — любой угол, выражение угла в радианной системе:

sin (π+α)=－sinα.

cos (π+α)=－cosα.

tg (π+α)=tgα.

ctg (π+α)=ctgα.

sec (π+α)=－secα.

cosec (π+α)=－cosecα.

В градусной мере:

sin (180°+α)=－sinα.

cos (180°+α)=－cosα.

tg (180°+α)=tgα.

ctg (180°+α)=ctgα.

sec (180°+α)=－secα.

cosec (180°+α)=－cosecα.

Связь между значением тригонометрической функции любого угла α и -α

Приведем формулы приведения, в которых устанавливается связь между значением тригонометрической функции любого угла α и угла -α:

sin (-α) = — sinα.

cos (-α) = cosα.

tg (-α) = — tgα.

ctg (-α)=ctgα.

sec (-α) = secα.

cosec (-α) = — cosecα.

Связь между значениями тригонометрических функций π-α и α

Эти формулы могут быть получены по формулам связи между значениями тригонометрических функций углов α и -α и между значением тригонометрической функции π + α и значением тригонометрической функции α :

Представление угла в радианной мере:

sin (π － α) = sinα.

cos (π － α) = — cosα.

tg (π － α) = — tgα.

ctg (π － α) = — ctgα.

sec (π － α) = — secα.

cosec (π － α) = cosecα.

Представление угла в градусной мере:

sin (180 ° －α) = sinα.

cos (180 ° －α) = — cosα.

tg (180 ° －α) = — tgα.

ctg (180 ° －α) = — ctgα.

sec（180 ° －α) = — secα.

cosec (180 ° －α) = cosecα.

Связь между значением тригонометрической функции 2π-α и α

Эти формулы могут быть получены по формулам связи тригонометрических функций аргументов противоположных на круг и угла α и угла -α :

Представление угла в радианной мере:

sin (2π － α) = — sinα.

cos (2π － α) = cosα.

tg (2π － α) = — tgα.

ctg (2π － α) = — ctgα.

sec (2π － α) = secα.

cosec (2π － α) = — cosecα.

Представление в градусной мере:

sin (360 ° －α) = — sinα.

cos （360 ° －α） = cosα.

tg (360 ° －α) = -tgα.

ctg (360 ° －α) = — ctgα.

sec（360 ° －α） = secα.

cosec (360 ° －α) = — cosecα.

Связь между значениями тригонометрических функций π/2 ± α и 3π/2 ± α и α

Связь между π / 2 + α и значением тригонометрической функции α

Представление угла в радианной мере:

sin (π / 2 + α) = cosα.

cos (π / 2 + α) = — sinα.

tg (π / 2 + α) = — ctgα.

ctg (π / 2 + α) = — tgα.

sec (π / 2 + α) = — cosecα.

cosec (π / 2 + α) = secα.

Представление угла в градусах:

sin (90 ° + α) = cosα.

cos (90 ° + α) = — sinα.

tg (90 ° + α) = -ctgα.

ctg (90 ° + α) = -tgα.

sec (90 ° + α) = -cosecα.

cosec (90 ° + α) = secα.

Связь между π / 2-α и значением тригонометрической функции α

Представление угла в радианной системе:

sin (π / 2 － α) = cosα.

cos (π / 2 － α) = sinα.

tg (π / 2 － α) = ctgα.

ctg (π / 2 － α) =tgα.

sec (π / 2 － α) = cosecα.

cosec (π / 2 － α) = secα.

Представление угла в градусах:

sin (90 ° －α) = cosα.

cos (90 ° －α) = sinα.

tg (90 ° －α) = ctgα.

ctg (90 ° －α) = tgα.

sec (90 ° －α) = cosecα.

cosec (90 ° －α) = secα.

Связь между 3π / 2 + α и значением тригонометрической функции α

Представление угла в радианах:

sin (3π / 2 + α) = — cosα.

cos (3π / 2 + α) = sinα.

tg (3π / 2 + α) = — ctgα.

ctg (3π / 2 + α) = -tgα.

sec (3π / 2 + α) = cosecα.

cosec (3π / 2 + α) = — secα.

Представление угла в градусах:

sin (270 ° + α) = — cosα.

cos (270 ° + α) = sinα.

tg (270 ° + α) = -ctgα.

ctg（270 ° + α） = -tgα.

sec (270 ° + α) = cosecα.

cosec (270 ° + α) = — secα.

Связь между 3π / 2 － α и значением тригонометрической функции α

Представление угла в радианах:

sin (3π / 2- α) = — cosα.

cos (3π / 2 -α) = — sinα.

tg (3π / 2 － α) =ctgα.

ctg (3π / 2 — α) =tgα.

sec (3π / 2 － α) = -cosecα.

cosec (3π / 2 － α) = — secα.

Представление угла в градусах:

sin (270 ° －α) = — cosα.

cos (270 ° －α) = — sinα.

tg（270 ° －α） = tgα.

ctg（270 ° －α） =tgα.

sec (270 ° －α) = -cosecα.

cosec (270 ° －α) = — secα.

Правило определения приведенной функции

Приведенные выше формулы приведения можно резюмировать так: для значения тригонометрической функции kπ / 2 ± α (k∈Z),

Когда k — четное число, значение приведенной функции будет с тем же именем, что и приводимая функция, но для α (острый угол), то есть имя функции не изменяется
Когда k — нечетное число, мы возьмем ко-функцию, но уже для α (острый угол), а именно sin (kπ / 2 ± α) → cosα; cos (kπ / 2 ± α) → sinα; tg (kπ / 2 ± α) → ctgα, ctg (kπ / 2 ± α) → tgα.

Запомни

Перед приведенной функцией мы должны добавить знак приводимой функции.

То есть мы получим:

$\ sin(2\pi k+\alpha)=\sin \alpha$ (1)

$\cos(2 \pi k + \alpha)=\cos \alpha$ (2)

Правило лошади в тригонометрии

Математики придумывают все новые и новые способы заставить ученика выучить это несложное правило, что придумали даже «кивающую лошадь». А правило, которое с ее помощью легче запомнить — это как раз вторая часть правила, когда k — нечетное число. В этом случае угол отсчитывается по вертикали. И тогда воображаемая лошадь кивает головой и функция меняется на ко-функцию. На наш взгляд абсолютно лишняя информация. Но если вам удобно — пользуйтесь.

Например:

sin (2π-α) = sin (4 · π/2-α), k = 4 — четное число, поэтому берется та же функция sinα.

Когда α — острый угол, 2π-α∈ (270°, 360°), sin (2π-α) <0 и поэтому перед функций мы поставим знак «-».

Итак, sin (2π－α) = — sinα.

sin (α+ π) = — sinα

Углы, фигурирующие во всех формулах приведения тригонометрических функций, сначала рассматриваются как острые углы, α + π — это угол в третьей четверти, а синус в третьей четверти отрицательный, поэтому конечный результат отрицательный, а π является четным кратным π/2, поэтому функция остается неизменной.

Чтобы определить знак приводимой функции, нарисуйте тригонометрический круг и вспомните знаки тригонометрических функций в координатных четвертях.

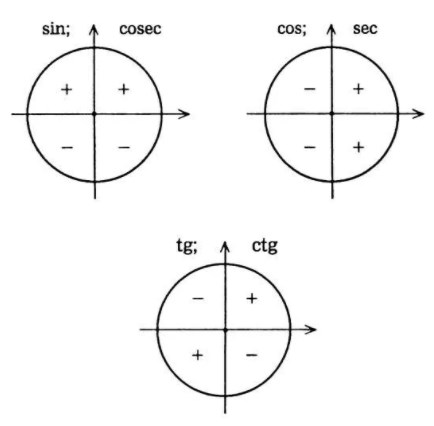
Формулы приведения в тригонометрии таблица

Все формулы приведения тригонометрических функций можно собрать в одну таблицу.

Угол	Функция
Угол	sinх	cosх	tgх	ctgх
α	sinα	cosα	tgα	ctgα
-α	-sinα	cosα	-tgα	-ctgα
π / 2 — α	cosα	sinα	ctgα	tgα
π / 2 + α	cosα	-sinα	-ctgα	-tgα
π－α	sinα	-cosα	-tgα	-ctgα
π + α	-sinα	-cosα	tgα	ctgα
3π / 2 -α	-cosα	-sinα	ctgα	tgα
3π / 2+α	-cosα	sinα	-ctgα	-tgα
2π-α	-sinα	cosα	-tgα	-ctgα
2π+α	sinα	cosα	tgα	ctgα

Формулы и правило приведения тригонометрических функций часто используются при решении тригонометрических уравнений и неравенств.

Примеры применения формул приведения

Пример 1

Вычислите $\sin 930^{\circ}$ .

Решение: Выделим целое количество тригонометрических кругов, каждый из которых $360^{\circ}$ . Получим: $\sin 930^{\circ}= \sin {(2 \cdot 360^{\circ}+210^{\circ})}$ По формуле приведения из таблицы находим: $\sin{(2 \cdot 360^{\circ}+210^{\circ})}=-\sin 210^{\circ}$

$\sin 210^{\circ}=\sin{(180^{\circ}+30^{\circ})}=-\sin30^{\circ}$ , подставляем $\sin{(2 \cdot 360^{\circ}+210^{\circ})}=-\sin 210^{\circ}=-(-\sin30^{\circ})=\sin30^{\circ}=\frac{1}{2}=0,5$ .

Пример 2

Вычислите $\cos 150^{\circ}$ .

Решение: Представим, $\cos 150^{\circ}=\cos{(90^{\circ}+60^{\circ})}$ .

Для решения воспользуемся правилом, так как у нас получается нечетное число k и функция поменяется на ко-функцию, то есть был косинус, станет синус. Определимся со знаком, посмотрим, в какую четверть попадает $\cos{(90^{\circ}+60^{\circ})}$ — это вторая четверть, косинус во второй четверти отрицательный, значит перед синусом поставим знак минус (ставим знак приводимой функции, а приводим мы косинус):

$\cos{(90^{\circ}+60^{\circ})}=-\sin 60^{\circ}=-\frac{\sqrt{3}}{2}$ .

Пример 3

Вычислите $\sin 135^{\circ}$ .

Решение: Проведем преобразования и применим правило приведения тригонометрических функций $\sin (90^{\circ}+45^{\circ})=\cos 45^{\circ}=\frac{\sqrt{2}}{2}$ .

Пример 4

Используя формулы приведения, вычислить:

$tg{\frac{5\pi}{4}}$ .

Решение:

Представим $\frac{5\pi}{4}=\frac{4\pi+\pi}{4}=\pi+\frac{\pi}{4}$

Тогда, $tg{\frac{5\pi}{4}}=tg{\pi+\frac{\pi}{4}}=tg{\frac{\pi}{4}}=1$

Ответ: $tg{\frac{5\pi}{4}}=1$ .

Пример 5

Упростите выражение:

${\Hugo \frac{ctg(\frac{\pi}{2}-\alpha)-tg (\pi+\alpha)+\sin (\frac{3\pi}{2}-\alpha)}{\cos(\pi+\alpha)}}$ .

Решение:

Приведем тригонометрические функции согласно правилу приведения, получим:

${\Hugo \frac{ctg(\frac{\pi}{2}-\alpha)-tg (\pi+\alpha)+\sin (\frac{3\pi}{2}-\alpha)}{\cos(\pi+\alpha)}} = {\Hugo \frac{tg \alpha-tg \alpha-\cos \alpha}{- \cos \alpha}}=\frac{-\cos \alpha}{-\cos \alpha}=1$ .

Ответ: $1$

Таким образом, чтобы правильно выполнить приведение тригонометрической функции большого угла к тригонометрической функции меньшего угла вы можете использовать формулы приведения, которые нужно будет выучить наизусть, а их свыше 50, можно облегчить себе запоминание — выучив таблицу. Или же воспользоваться простым правилом (рекомендуется). Удачи на экзаменах.