На предыдущих занятиях мы решали графическим способом тригонометрические неравенства вида:
- sint < a (10.2.1. Решение тригонометрических неравенств. Часть 1.)
- sint > a (10.2.2. Решение тригонометрических неравенств. Часть 2.)
- cost < a (10.2.3. Решение тригонометрических неравенств. Часть 3.)
- cost > a (10.2.4. Решение тригонометрических неравенств. Часть 4.)
На этом занятии мы решим три неравенства вида: tgt < a.
Составим алгоритм решения.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=tgt и y=a.
3. Находим промежуток значений t, при которых тангенсоида располагается ниже прямой у=а. Левая граница этого промежутка всегда (-π/2), а правая arctg a
4. Записываем двойное неравенство для аргумента t, учитывая период тангенса Т=π (t будет между абсциссами(-π/2) и arctg a).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Решение тригонометрических неравенств графическим способом надежно страхует нас от ошибок только в том случае, если мы грамотно построим графики.
Первое неравенство
Построим графики функций y=tgx и у=1. Подробно рассмотрим построение тангенсоиды. Приготовим координатную плоскость хОу следующим образом:
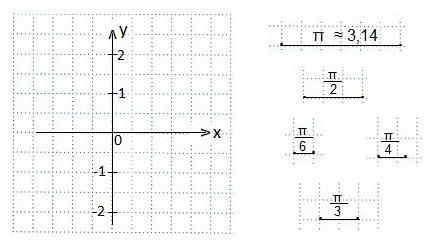
единичный отрезок равен двум клеткам; так как значение π≈3,14, то π на горизонтальной оси Ох будет изображаться шестью клетками; половина π (это π/2) — тремя клетками. Одна клетка — это π/6; полторы клетки — это π/4; две клетки будут соответствовать аргументу π/3.
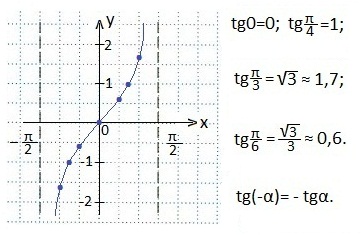
Мы знаем, что тангенс 90° не существует, а так как функция тангенса периодическая с наименьшим периодом, равным π, то не существует тангенс (90°+πn). Учтем это при построении графика и проведем две асимптоты: х= - π/2 и х=π/2.
Итак, в промежутке от - π/2 до π/2 тангенс будет «пробегать» все свои значения. Пользуясь значениями тангенса некоторых углов и свойством нечетности функции тангенса (график будет симметричен относительно начала координат), строим точки в приготовленной координатной плоскости, через которые и проведем тангенсоиду.
Построим прямую у=1.
Проведем ее параллельно оси Ох, выше на один единичный отрезок (выше на 2 клетки).
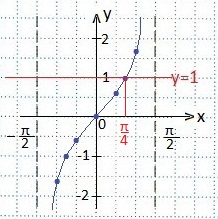
Прямая у=1 пересекает тангенсоиду в точке с координатами (π/4; 1).
Определяем промежуток значений х, при которых неравенство будет верным, т.е. внутри которого тангенсоида располагается ниже прямой у=1. Учтем, что неравенство нестрогое, значит, правый конец промежутка (π/4) входит во множество решений неравенства. Записываем решение в виде двойного неравенства. Ответ запишем в виде промежутка.
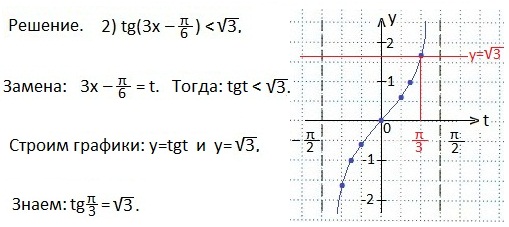
Второе неравенство
Отметим промежуток значений t, при которых точки тангенсоиды находятся ниже точек прямой у=1. Запишем этот промежуток в виде двойного неравенства. Затем перезапишем его для первоначального аргумента и выразим х. Ответ запишем в виде промежутка.
Третье неравенство
Отмечаем промежуток значений t, при которых неравенство верно. У нас нестрогое неравенство, значит, правый конец промежутка значений t также является решением неравенства. Возвращаемся к первоначальному аргументу и выражаем х. Ответ записываем в виде промежутка значений переменной х.
Смотреть видео: «10.2.5. Решение тригонометрических неравенств. Часть 5.»
Неравенства вида tgt < a можно решать и без графиков, по соответствующей формуле.
Если tgt < a, то — (π/2) + πn < t < arctg a + πn, где nєZ.

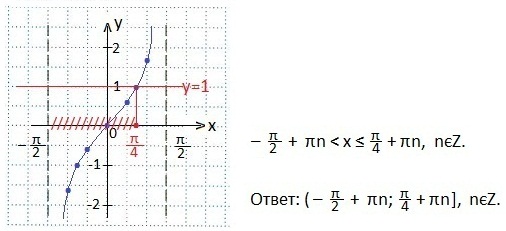

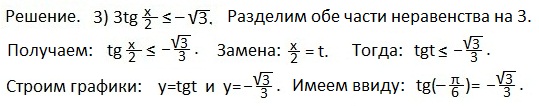


Классно объясняете