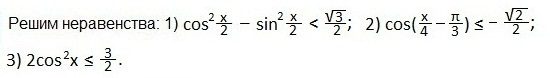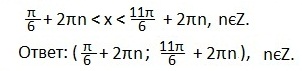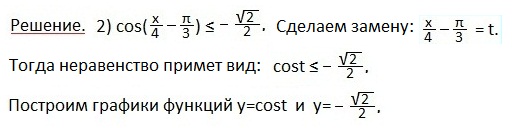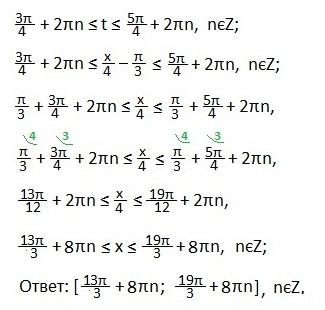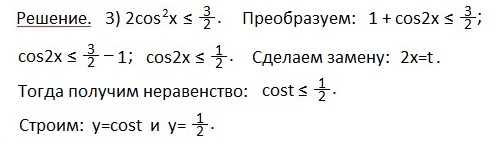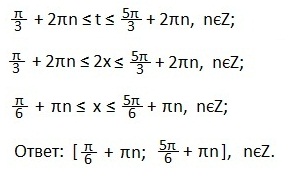На предыдущих двух занятиях по решению тригонометрических неравенств графическим способом мы рассмотрели решения неравенств вида:
- sint < a («10.2.1. Решение тригонометрических неравенств. Часть 1.»)
- sint > a («10.2.2. Решение тригонометрических неравенств. Часть 2.»)
Продолжаем решать тригонометрические неравенства графическим способом. Рассмотрим неравенства вида cost < a:
Составим алгоритм решения.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=cost и y=a.
3. Находим такие две соседние точки пересечения графиков, между которыми синусоида располагается ниже прямой у=а. Находим абсциссы этих точек.
4. Записываем двойное неравенство для аргумента t, учитывая период косинуса Т=2π (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Решение тригонометрических неравенств с помощью графиков надежно страхует нас от ошибок только в том случае, если мы грамотно построим синусоиду. (График функции y=cosx также называют синусоидой!)
Первое неравенство
Преобразуем левую часть неравенства по формуле косинуса двойного аргумента:
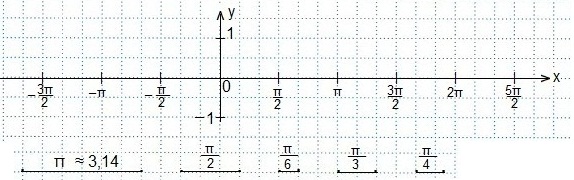
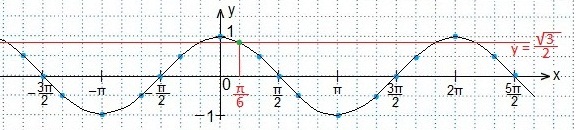
Координатную плоскость готовим так же, как готовили для построения графика функции y=sinx. (10.2.1. Решение тригонометрических неравенств. Часть 1), т.е. единичный отрезок берем равным двум клеткам, тогда значение π изображаем равным шести клеткам и т.д. Вот так должна выглядеть координатная плоскость для построения синусоид:
Воспользуемся таблицей значений косинусов некоторых углов:
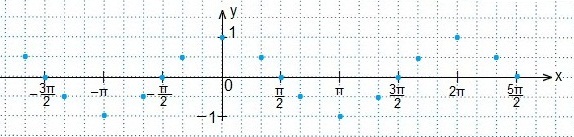
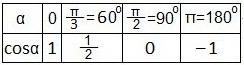а также свойствами: графиков четных функций, непрерывностью и периодичностью функции косинуса. Отмечаем точки:
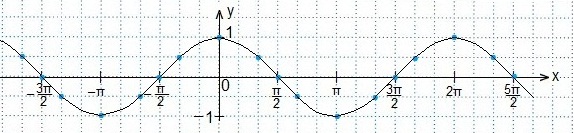
Проводим через эти точки кривую — график функции y=cosx.
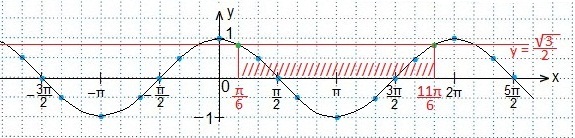
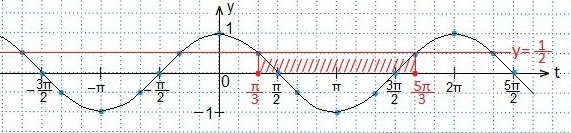
Определяем промежуток значений х, при которых точки синусоиды лежат ниже точек прямой.
Учтем периодичность функции косинуса и запишем в виде двойного неравенства решение данного неравенства:
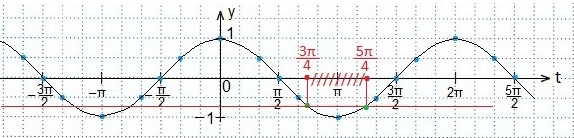
Второе неравенство
Находим абсциссы точек пересечения графиков, между которыми график косинуса лежит ниже прямой.
Концы этого промежутка тоже являются решениями неравенства, так как неравенство нестрогое.
Запишем решение в виде двойного неравенства для переменной t.
Подставим вместо t первоначальное значение аргумента.
Выразим х.
Ответ запишем в виде промежутка.
Третье неравенство
Смотрите видео: «10.2.3. Решение тригонометрических неравенств. Часть 3.»
А теперь формула, которой вам следует воспользоваться на экзамене ЕНТ или ЕГЭ при решении тригонометрического неравенства вида cost < a.
Если cost < a, (-1≤а≤1), то arccos a + 2πn < t < 2π — arccos a + 2πn, nєZ.
Примените эту формулу для решения рассмотренных в этой статье неравенств, и вы получите ответ гораздо быстрее и безо всяких графиков!
