10.3.0. Вычисление производных

На этом занятии мы будем учиться применять формулы и правила дифференцирования.

Примеры. Найти производные функций.

1. y=x⁷+x⁵-x⁴+x³-x²+x-9. Применяем правило I, формулы 4, 2 и 1. Получаем:

y’=7x⁶+5x⁴-4x³+3x²-2x+1.

2. y=3x⁶-2x+5. Решаем аналогично, используя те же формулы и формулу 3.

y’=3∙6x⁵-2=18x⁵-2.

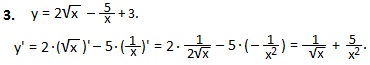Применяем правило I,  формулы 3, 5 и 6 и 1.

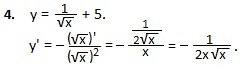 Применяем правило IV, формулы 5 и 1.

В пятом примере по правилу I производная суммы равна сумме производных,  а производную 1-го слагаемого мы только что находили (пример 4), поэтому, можем сразу писать результат.

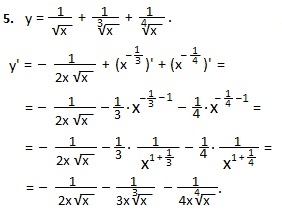Дифференцируем 2-ое и 3-е слагаемые по формуле 4. Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями.

Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.

Решим шестой пример и выведем еще одну  формулу.

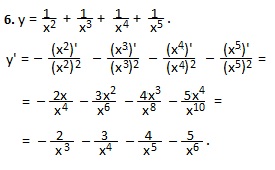Используем правило IV и формулу 4. Получившиеся дроби сократим.

Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:

Учим новые формулы!