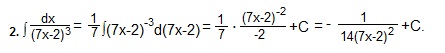На прошлом занятии (11.1.2), рассматривая примеры на нахождение неопределенных интегралов, мы познакомились со способом подведения под знак дифференциала (мы называли его вторым способом). Фактически мы вводили новую переменную, не называя ее, а только подразумевая.
На этом занятии мы закрепим навык замены переменной в неопределенном интеграле и знания свойств и таблицы интегралов. Нам опять понадобится наш лист Интегралы.
Рассмотрим примеры поиска неопределенных интегралов.
Пример 1
1. ∫(6х+5)3dx. Как будем решать? Смотрим в лист Интегралы и рассуждаем примерно так: подынтегральная функция представляет собой степень, а у нас есть формула для интеграла степени (формула 1)), но в ней основание степени u и переменная интегрирования тоже u.
А у нас переменная интегрирования х, а основание степени (6х+5). Сделаем замену переменной интегрирования: вместо dx запишем d (6х+5). Что изменилось? Так как, то, что стоит после знака дифференциала d, по умолчанию, дифференцируется,
то d (6x+5)=6dx, т.е. при замене переменной х на переменную (6х+5) подынтегральная функция возросла в 6 раз, поэтому перед знаком интеграла ставим множитель 1/6. Записать эти рассуждения можно так:
Итак, мы решили этот пример введением новой переменной (переменную х заменили на переменную 6х+5). А куда записали новую переменную (6х+5)? Под знак дифференциала. Поэтому, данный метод введения новой переменной часто называют методом (или способом) подведения (новой переменной) под знак дифференциала.
Пример 2
Во втором примере мы вначале получили степень с отрицательным показателем, а затем подвели под знак дифференциала (7х-2) и использовали формулу интеграла степени 1) (Интегралы).
Пример 3
Разберем решение примера 3.
Перед интегралом стоит коэффициент 1/5. Почему? Так как d (5x-2)=5dx, то, подведя под знак дифференциала функцию u=5x-2, мы увеличили подынтегральное выражение в 5 раз, поэтому, чтобы значение данного выражения не изменилось — надо было разделить на 5, т.е. умножить на 1/5. Далее, была использована формула 2) (Интегралы).