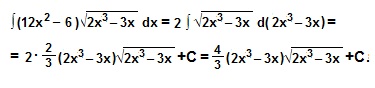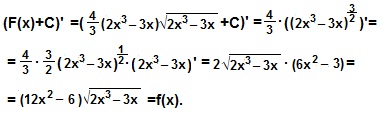При интегрировании путем подведения под знак дифференциала, в предыдущих занятиях, мы подводили под знак дифференциала линейную функцию. На самом деле, вместо переменной u мы каждый раз подразумевали выражение вида kx+b, т.е. полагали: u-kx+b, получали du=kdx, а затем перед знаком интеграла ставили коэффициент 1/k, чтобы не изменилось значение данного интеграла. При решении использовали свойства и таблицу интегралов — лист Интегралы.
А можно ли под знак дифференциала подводить нелинейную функцию? Да, если подынтегральное выражение представляет собой произведение двух множителей: один множитель — сложная функция от какой-то нелинейной функции, а другой множитель есть производная от этой нелинейной функции. Рассмотрим сказанное на примерах.
Найти неопределенные интегралы.
Пример 1
∫(2x + 1)(x2 + x + 2)5 dx = ∫(x2 + x + 2)5 d (x2 + x + 2) =(x²+x+2)6:6 + C.
Что представляет собой данное подынтегральное выражение? Произведение степенной функции от (х2 + х + 2) и множителя (2х + 1), который равен производной от основания степени: (х2 + х + 2)' = 2х + 1.
Это и позволило нам подвести (2х + 1) под знак дифференциала:
(2x + 1) dx = d (x2 + x + 2). А далее мы применили формулу:
∫u5du=u6:6+ C. (Формула 1). Интегралы)
Проверка. (F (x)+ C)' =((x²+x+2)6:6 + C)′=1/6 · 6 (x2 + x + 2)5 · (x2 + x + 2)' =
=(x2 + x + 2)5 · (2x + 1) = (2x + 1)(x2 + x + 2)5 = f (x).
Пример 2
∫(3x2 – 2x + 3)(x3 - x2 + 3x + 1)5 dx = ∫(x3 – x2 + 3x + 1)5 d (x3 – x2 + 3x + 1) =
=(x³- x²+3x+1)6:6 + C
И чем этот пример отличается от примера 1? Да ничем! Та же пятая степень с основанием (х3 – х2 + 3х + 1) умножается на трехчлен (3х2 – 2х + 3), который является производной основания степени: (х3 – х2 + 3х + 1)' = 3х2 – 2х + 3. Это основание степени мы и подвели под знак дифференциала, от чего значение подынтегрального выражения не изменилось, а затем применили ту же формулу 1). (Интегралы)
Пример 3
Здесь производная от (2х3 – 3х) даст (6х2 – 3), а у нас имеется (12х2 – 6), то есть выражение в 2 раза большее, значит, подведем (2х3 – 3х) под знак дифференциала, а перед интегралом поставим множитель 2. Применим формулу 2) (лист Интегралы).
Вот что получится:
Сделаем проверку, учитывая, что:
Итак,