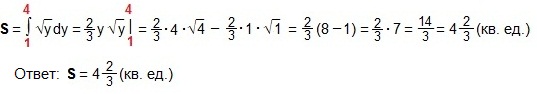Если криволинейная трапеция прилегает к оси Оу (рис. 1) и ограничена непрерывной кривой x=f (y), осью ординат (прямой х=0) и прямыми y=a, y=b, то ее площадь вычисляется по той же формуле Ньютона-Лейбница (ф. Н-Л), только переменная интегрирования не х, а у:
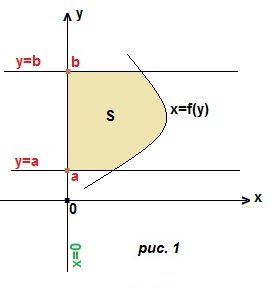
Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=x², y=1, y=4 и осью Оу.
Решение. Построим данную криволинейную трапецию (рис. 2). Выразим х через у:
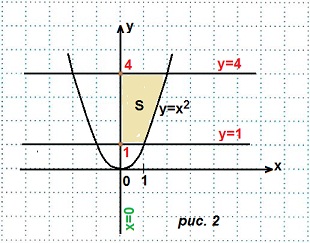
Искомую площадь S находим по формуле Ньютона-Лейбница (ф. Н-Л). У нас a=1, b=4.
