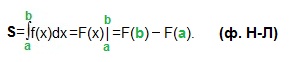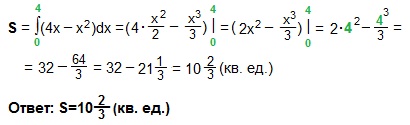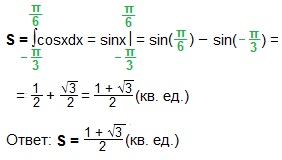Площадь криволинейной трапеции, ограниченной сверху графиком функции y=f (x), снизу — осью Ох, слева и справа прямыми х=a, x=b, находят по формуле Ньютона-Лейбница (ф. Н-Л):
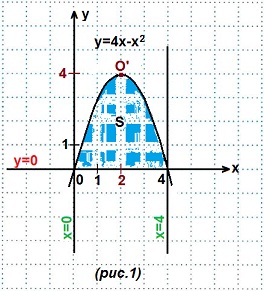Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=4x-x²; y=0; x=0; x=4.
Решение. Строим графики данных линий. (рис. 1).
1) y=4x-x² — парабола (вида y=ax²+bx+c). Запишем данное уравнение в общем виде: y=-x²+4x. Ветви этой параболы направлены вниз, так как первый коэффициент а=-1<0.
Вершина параболы находится
в точке O′(m; n), где
О′(2; 4). Нули функции (точки пересечения графика с осью Ох) найдем из уравнения:
4х-х²=0.
Выносим х за скобки, получаем: х(4-х)=0. Отсюда, х=0 или х=4. Абсциссы точек найдены, ордината равна нулю — искомые точки: (0; 0) и (4; 0).
2) y=0 — это ось Ох; 3) х=0 — это ось Оy; 4) х=4 — прямая, параллельная оси Оy и отстоящая от нее на 4 единичных отрезка вправо.
Площадь построенной криволинейной трапеции находим по (ф. Н-Л). У нас f (x)=4x-x², a=0, b=4.
Кстати, если Вы подсчитаете все целые заштрихованные клетки и добавите к ним половину всех остальных клеток заштрихованной фигуры, то получите приближенное значение искомой площади. Действительно, если единичный отрезок равен одной клетке, то площадь квадратика со стороной, равной 1 клетке, равна 1·1=1 (кв. ед.). Сколько квадратиков — столько квадратных единиц и составляет площадь фигуры.
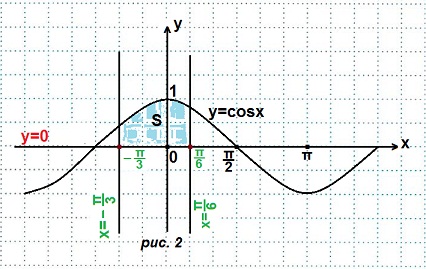
Пример 2. Найти площадь криволинейной трапеции, ограниченной линиями:
Решение. Строим графики данных линий. (рис. 2).
Площадь данной криволинейной трапеции:
