Цилиндр вписан в правильную четырехугольную призму

Цилиндр вписан в правильную четырехугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.

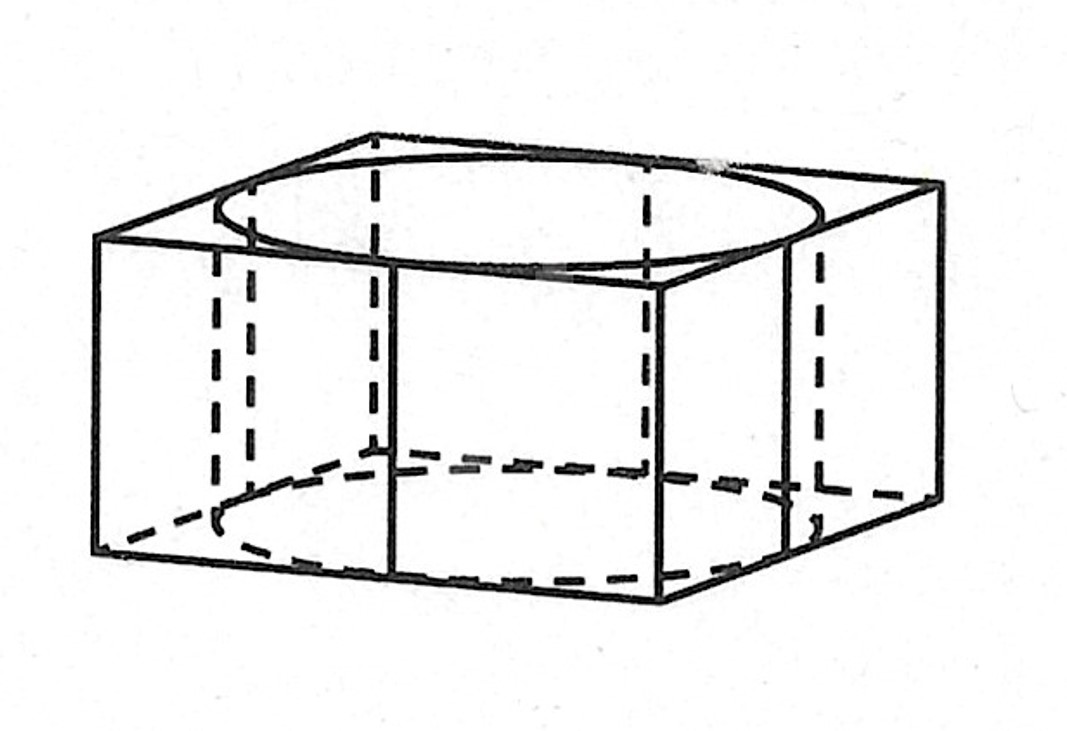
Решение: Площадь боковой поверхности призмы — это сумма площадей боковых прямоугольников. Для того, чтобы найти площадь прямоугольника нам надо знать его стороны. Высоту призмы мы уже знаем — это 3. Высота призмы равна высоте цилиндра, так как цилиндр вписан в призму, а значит, его основания содержатся в основаниях призмы.

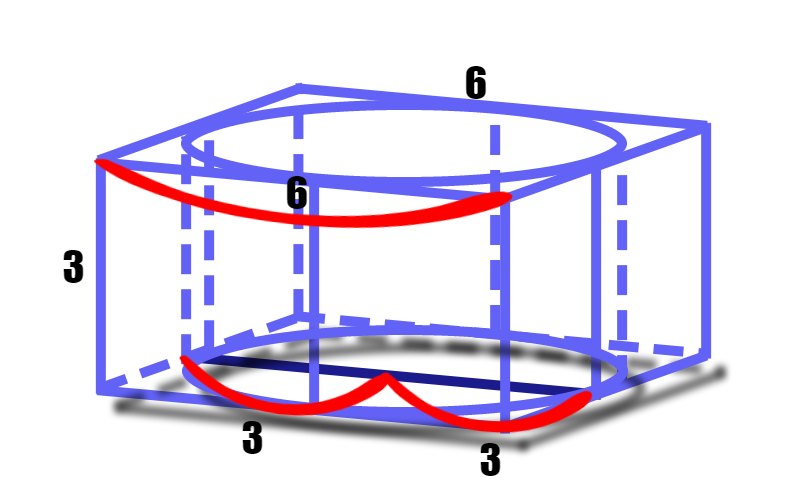
Отметим на рисунке диаметр основания цилиндра (темно-синяя линия). Очевидно, что диаметр основания цилиндра равен стороне боковой грани призмы. Таким образом, получаем, что ширина боковой грани призмы 6. Значит, площадь одной грани будет .

Таких  граней четыре. Значит надо 18 умножить на 4 и мы найдем площадь боковой поверхности призмы.

Ответ: 72