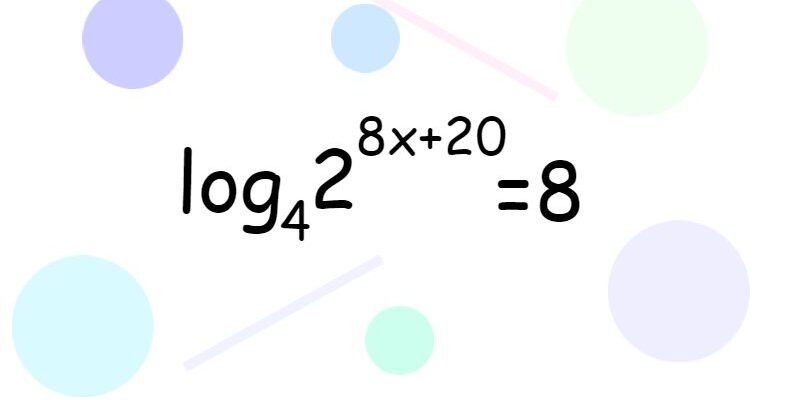Решите уравнение log 4 2^(8x+20)=8

Решите уравнение Log 4 2^(8x+20)=8 (1)

ЕГЭ по математике профильный уровень

На чтение 2 мин. Просмотров 3k.

Логарифмическое уравнение, которое легко решить, если знать свойства логарифмов. Рассмотрим два варианта решения этого уравнения.

Решите уравнение $\displaystyle \log_4 2^{8x+20}=8$

Решение (способ 1):

Приведем в правой части 8 к логарифму по основанию 2, и в левой части также преобразуем логарифм к логарифму по основанию 2. Воспользуемся следующими формулами:

$\displaystyle \log_{a^m}b=\frac{1}{m} \log b=\log b^{\frac{1}{m}}$

$\displaystyle a=a \log_b b=\log_b b^a$

Число 8 можно записать:

$\displaystyle 8=\log_2 2^8$

Левая часть уравнения будет преобразована таким образом:

$\displaystyle \log_{2^2} 2^{8x+20}=\log_{2^2} 2^{8x+20}=\frac{1}{2} \log_{2}2^{8x+20}=\log_2 2^{\frac{1}{2}(8x+20)}$

Тогда наше уравнение примет вид

$\displaystyle \log_2 2^{\frac{1}{2}(8x+20)}=\log_2 2^8$

Слева логарифм по основанию 2 и справа такой же логарифм по основанию 2. Значит, выражения под знаком логарифма также равны.

$\displaystyle 2^{\frac{1}{2}(8x+20)}=2^8$

Основания степени равны, значит, равны и показатели степени:

$\displaystyle \frac{1}{2}(8x+20)=8$

$\displaystyle 4x+10=8$

$\displaystyle 4x=8-10$

$\displaystyle 4x=-2$

$\displaystyle x=\frac{-2}{4}$

$\displaystyle x=\frac{-1}{2}=-0,5$

Ответ: -0,5

Решение (способ 2)

Задачу можно решить и проще, если использовать формулу:

$\displaystyle \log_b a^m=m \log_b a$

Тогда левая часть уравнения:

$\displaystyle \log_4 2^{8x+20}=(8x+20) \log_4 2=(8x+20)\frac{1}{2} \log _2 2=\frac{1}{2} (8x+20)$ так как $\log_2 2=1$

Тогда, получаем:

$\displaystyle \frac{1}{2} (8x+20)=8$

$\displaystyle 4x+10=8$

$\displaystyle x=-0,5$

Второй способ легче и быстрее приводит к результату. Не забывайте делать проверку.

Ответ: -0,5

( 4 оценки, среднее 5 из 5 )

0 комментариев

Межтекстовые Отзывы

Посмотреть все комментарии