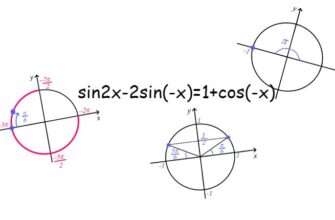Найдите корень уравнения (1/ 4)^(x+2)=256^x

Найдите корень уравнения (\frac{1}{4})^{x+2}=256^x

Решение:

Чтобы решить данное показательное уравнение приведем справа и слева степени к одному основанию. Удобнее взять основание 4.

Тогда преобразуем левую часть уравнения:

\displaystyle (\frac{1}{4})^{x+2}=4^{- (x+2)}

В правой части уравнения стоит число 256. Это 4 в какой степени? Чтобы это выяснить, будем последовательно делить 256 на 4:

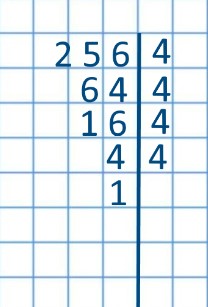
Справа от вертикальной черты четыре четверки, то есть 256=4·4·4·4, значит 256=4⁴.

Итак, наше уравнение теперь можно записать в виде:

4^{- (x+2)}=4^{4x}

Основания степеней равны, значит, равны и показатели степеней.

— (x+2)=4x
-x-2=4x
-x-4x=2
-5x=2
\displaystyle  x=\frac{-2}{5}
x=-0,4

Обязательно сделайте проверку.

Ответ: -0,4.