Моторная лодка прошла против течения реки 96 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 10 км/ч. Ответ дайте в км/ч. Задача взята из типовых экзаменационных вариантов по математике профильного уровня за 2023 год, выпущенных под редакцией И.В. Ященко. Решения в этих материалах данной задачи нет, поэтому мы решим эту задачу с подробным объяснением.
Решение
Вспомним как мы записываем скорость лодки при движении по течению и при движении против течения.
Если ввести следующие обозначения ![]() — скорость течения реки,
— скорость течения реки, ![]() — собственная скорость лодки (скорость лодки в неподвижной воде или когда течение ничтожно мало и им можно пренебречь), то скорость лодки при движении по течению
— собственная скорость лодки (скорость лодки в неподвижной воде или когда течение ничтожно мало и им можно пренебречь), то скорость лодки при движении по течению ![]() , а скорость лодки против течения будет
, а скорость лодки против течения будет ![]() .
.
Нам в задаче дана собственная скорость лодки ![]() км/ч.
км/ч.
Пусть скорость течения будет x, тогда скорость моторной лодки при движении против течения реки будет ![]() , а скорость моторной лодки при движении по течению реки будет
, а скорость моторной лодки при движении по течению реки будет ![]() .
.
Нарисуем таблицу.
| Направление движения лодки | Скорость | Время | Расстояние, |
| Против течения реки | 96 | ||
| По течению реки | 96 |
Таблица заполняется с учетом формулы ![]() , в задаче даны скорость и расстояние, а время мы можем сами получить, используя формулу
, в задаче даны скорость и расстояние, а время мы можем сами получить, используя формулу ![]() .
.
Нам также известно, что на обратный путь моторная лодка затратила на 4 часа меньше. То есть время движения по течению реки было на 4 часа меньше, чем время движения против течения реки. Получим уравнение:
![]() , сократив левую и правую часть уравнения на 4, получим
, сократив левую и правую часть уравнения на 4, получим
![]()
![]()
![]() , так как
, так как ![]() — можно упростить используя формулу разности квадратов:
— можно упростить используя формулу разности квадратов: ![]() .
.
![]()
![]()
Решим полученное квадратное уравнение, используя теорему Виета:
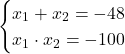
Подбирая, получим ![]() ,
, ![]() .
.
Так как скорость течения реки не может быть отрицательным числом, возьмем значение ![]() .
.
Выполним проверку:
![]()
![]()
![]()
![]()
Ответ: 2 км/ч — скорость течения реки. В ответ мы запишем только число 2.









