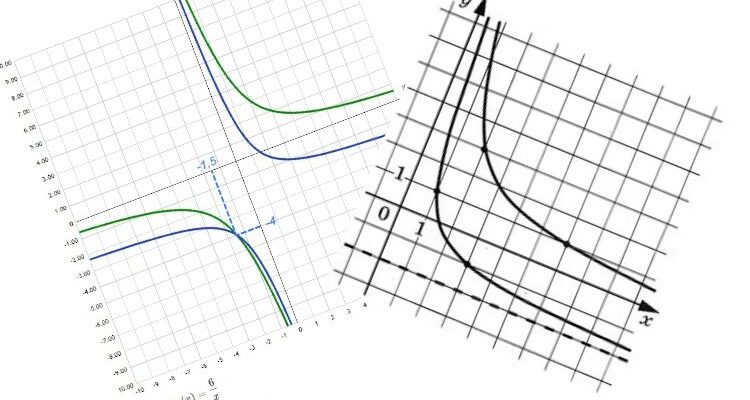
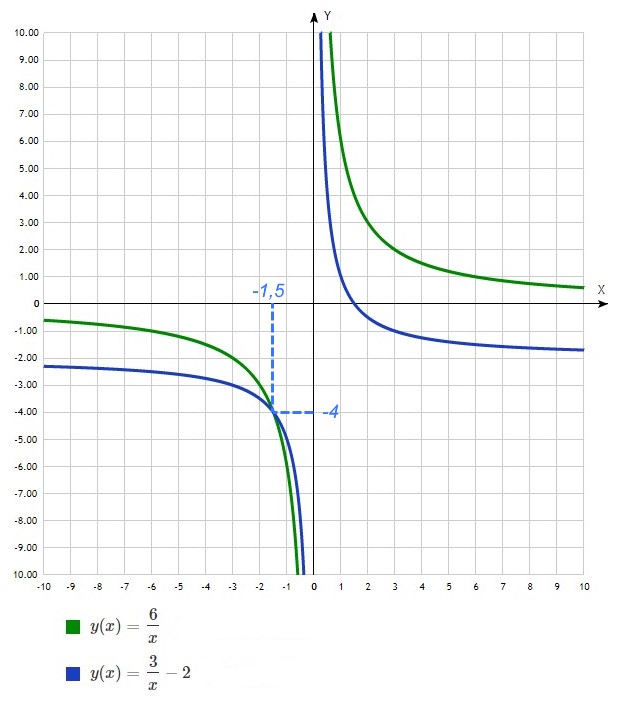
На рисунке изображены части графиков функций ![]() и
и ![]() . Найдите ординату точки пересечения графиков этих функций.
. Найдите ординату точки пересечения графиков этих функций.
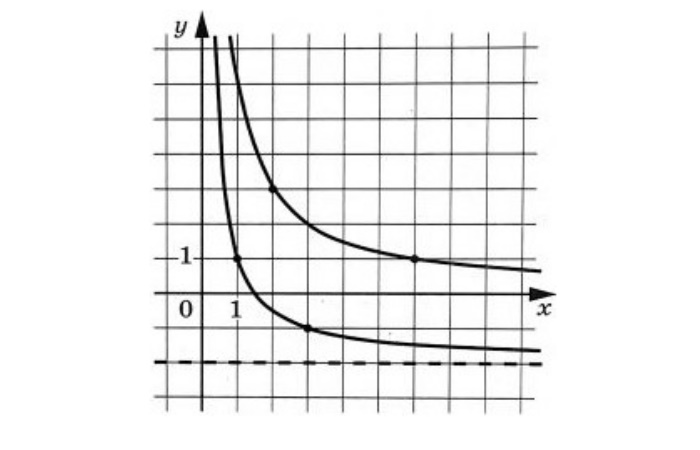
Решение:
Верхний график на рисунке не пересекает ось Ox, значит не имеет смещения вдоль оси Oy. Поэтому он принадлежит первой функции ![]() . Тогда второй (нижний) график на картинке принадлежит функции
. Тогда второй (нижний) график на картинке принадлежит функции ![]() так как пересекает ось Ox, а значит, работает коэффициент
так как пересекает ось Ox, а значит, работает коэффициент ![]() , смещающий график вниз.
, смещающий график вниз.
Для первого графика даны точки ![]() и
и ![]() , а для второго графика:
, а для второго графика: ![]() и
и ![]() . Они нам помогут определить коэффициенты
. Они нам помогут определить коэффициенты ![]() ,
, ![]() ,
, ![]() .
.
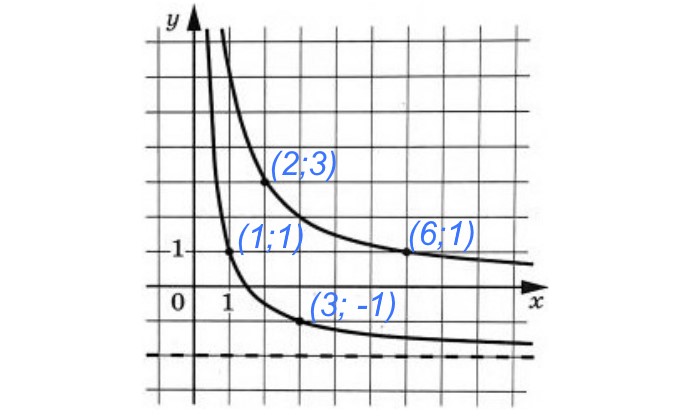
Кстати, коэффициент ![]() вы можете определить сразу по графику, видно что ассимптота графика (на графике показана пунктирной линией) смещена вниз на 2 деления (по сравнению со стандартным графиком параболы, где ассимптота совпадает с осью абсцисс) и совпадает с прямой
вы можете определить сразу по графику, видно что ассимптота графика (на графике показана пунктирной линией) смещена вниз на 2 деления (по сравнению со стандартным графиком параболы, где ассимптота совпадает с осью абсцисс) и совпадает с прямой ![]() . Таким образом, можно сразу сказать, что
. Таким образом, можно сразу сказать, что ![]() .
.
Подставим значения первой точки ![]() в уравнение
в уравнение ![]() и найдем
и найдем ![]() :
:
![]()
![]() .
.
Выполним проверку, подставим теперь уже в определенной уравнение функции ![]() координаты второй точки
координаты второй точки ![]() :
:
![]()
![]() .
.
Итак, с первой функцией определились. Теперь определим и вторую. Поскольку во второй функции у нас два неизвестных ![]() и
и ![]() , то нам понадобится система из двух уравнений. Первое уравнение мы получим, подставив координаты первой точки
, то нам понадобится система из двух уравнений. Первое уравнение мы получим, подставив координаты первой точки ![]() , а второе уравнение получим, подставив координаты второй точки
, а второе уравнение получим, подставив координаты второй точки ![]() .
.
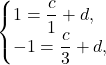
Из первого уравнения системы выразим ![]() :
:
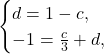
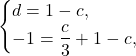
Решаем второе уравнение системы:
![]()
![]()
![]()
Получим:
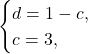
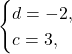
Тогда уравнение второй функции будет иметь вид: ![]()
Получили две функции ![]() и
и ![]() . В точке пересечения графиков функций значения их совпадают, значит,
. В точке пересечения графиков функций значения их совпадают, значит, ![]() , получим уравнение:
, получим уравнение:
![]()
![]()
![]()
![]() .
.
Мы нашли абсциссу точки пересечения, но нам надо найти ординату этой точки. Подставим полученное значение в любое из уравнений ![]() или
или ![]() .
.
![]() .
.
Ответ: -4.