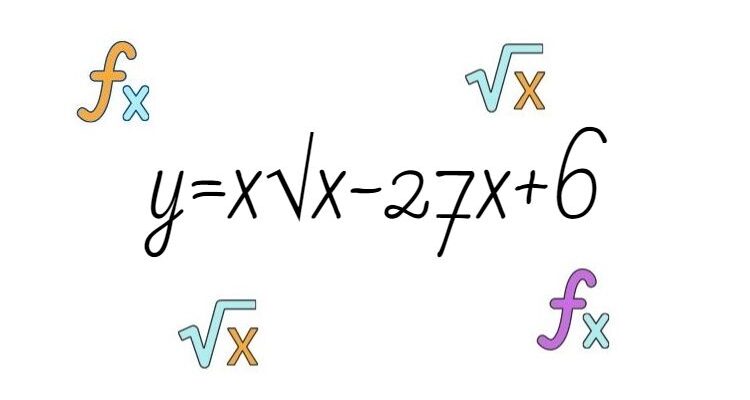Найдите наименьшее значение функции y=x√x-27x+6 на отрезке [1; 422]

На чтение 3 мин. Просмотров 4.4k.

Найдите наименьшее значение функции $y=x \sqrt{x}-27x+6$ на отрезке [1; 422].

Решение: Мы знаем, что для того, чтобы найти наименьшее значение функции на отрезке, нам необходимо определить критические точки функции.

Критические точки функции — это те точки, где на графике функции наблюдается максимум или минимум. В этих точках производная функции равна нулю.

Если такая точка попадет внутрь отрезка, то мы определим в ней значение функции. Еще мы подсчитаем значение функции на концах отрезка, то есть определим $y(1)$ и $y(422)$ . Сравним все полученные значения функции — в критических точках, в точках начала и конца отрезка и среди этих значений выберем наименьшее. Таков наш план.

Теперь начнем определять критические точки функции, для этого найдем ее производную.

$y'(x)= (x \sqrt{x}-27x+6)'=(x\sqrt{x})'-(27x)'+6'=(x^{\frac{3}{2}})'-27=\frac{3}{2} \cdot x^{\frac{1}{2}}-27$

Здесь мы заменили произведение $x \sqrt{x}=x \cdot x^{\frac{1}{2}}=x^{1+\frac{1}{2}}=x^{\frac{3}{2}}$ — все-таки находить производную от произведения сложнее, чем производную от степени. Упростили себе задачу.

Теперь приравняем производную к нулю:

$y'(x)=0$

$\frac{3}{2} \cdot x^{\frac{1}{2}}-27=0$

$\sqrt{x}=18$

$x=18^2$

$x=324$ .

Мы нашли критическую точку $x=324$ , она лежит внутри отрезка [1,422]. Теперь посмотрим, какое будет значение функции в этой точке: $y(324)=324 \cdot \sqrt{324}-27\cdot 324+6=18 \cdot 324 - 27 \cdot 324 +6=-9 \cdot 324 +6=-2910$ .

Теперь определим какие значения принимает функция на границах отрезка:

$y(1)=1-27+6=-20$
$y(422)=422 \sqrt{422}-27 \cdot 422+6 \approx 8669-11394+6 \approx -2719$ .

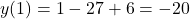
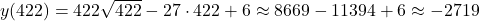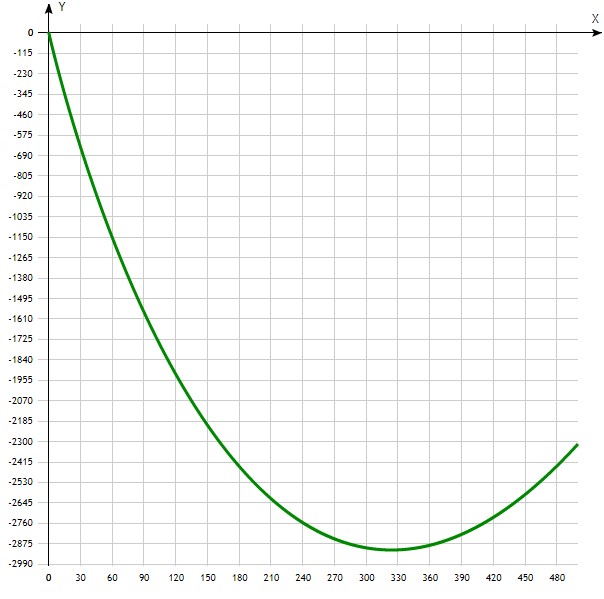
Получается, что значение функции -2910 является наименьшим, среди трех значений. Конечно, на экзамене нарисовать функцию не получится, разве что схематически, но мы решили в рамках объяснения нарисовать вам эту функцию, чтобы вы могли увидеть — что значение в точке $x=324$ действительно наименьшее.

Ответ: -2910.