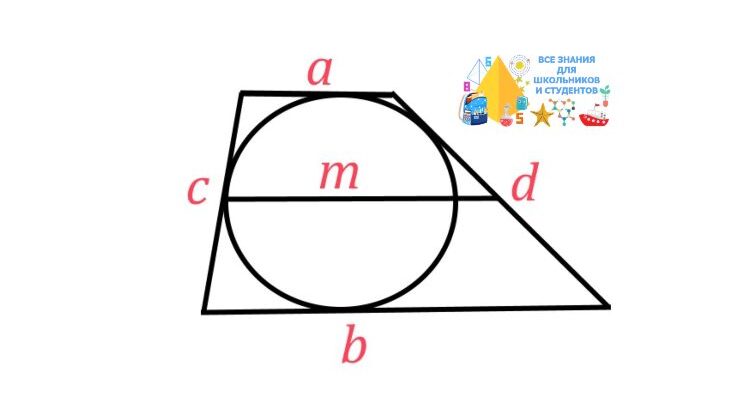
Около окружности описана трапеция, периметр которой равен 30

Около окружности описана трапеция периметр которой равен 30 (1)

ЕГЭ по математике профильный уровень

На чтение 2 мин. Просмотров 3k.

Простая задача по геометрии из сборника типовых заданий ЕГЭ. Простая - если знать свойство четырехугольника, в который вписана окружность. А если не знать - практически нерешаемая.

Около окружности описана трапеция, периметр которой равен 30. Найдите длину ее средней линии.

Решение: Не в каждую трапецию можно вписать окружность. Если это возможно, то стороны такой трапеции обладают следующим свойством:

В трапецию можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон трапеции равны: $a+b=c+d$

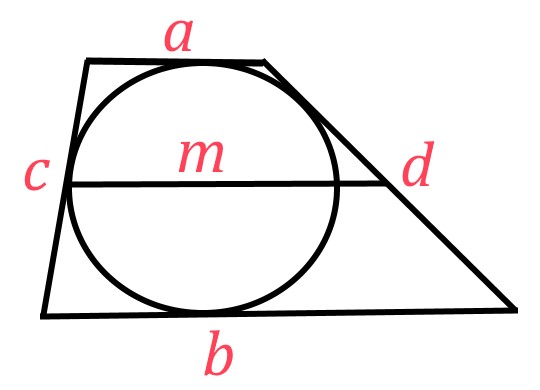
Таким образом, сумма длин сторон трапеции равна половине ее периметра. Так как $a+b=c+d$ , и $a+b+c+d=30$ . Заменим $c+d$ на $a+b$ , получим:

$a+b+a+b=30$

или

$2a+2b=30$

или $2(a+b)=30$ .

Отсюда:

$a+b=15$ .

Так как средняя линия трапеции равна половине суммы ее оснований, то находим:
$m=\displaystyle \frac{a+b}{2}=\frac{15}{2}=7,5$ .

Ответ: 7,5

( 1 оценка, среднее 5 из 5 )

0 комментариев

Межтекстовые Отзывы

Посмотреть все комментарии