Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 18,5

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 18,5. Объем параллелепипеда равен 5476. Найдите высоту цилиндра.

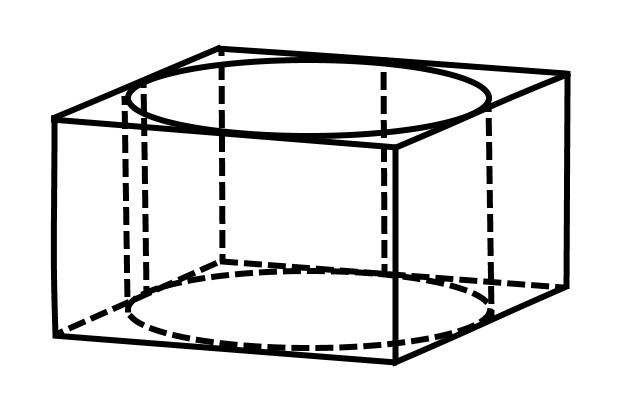
Решение: Так как цилиндр вписан в параллелепипед, то и основание цилиндра (круг) вписано в основание параллелепипеда (прямоугольник).

Поскольку вписать в четырехугольник окружность можно тогда и только тогда, когда суммы противоположных сторон четырехугольника равны, то перед нами не прямоугольник, а квадрат.

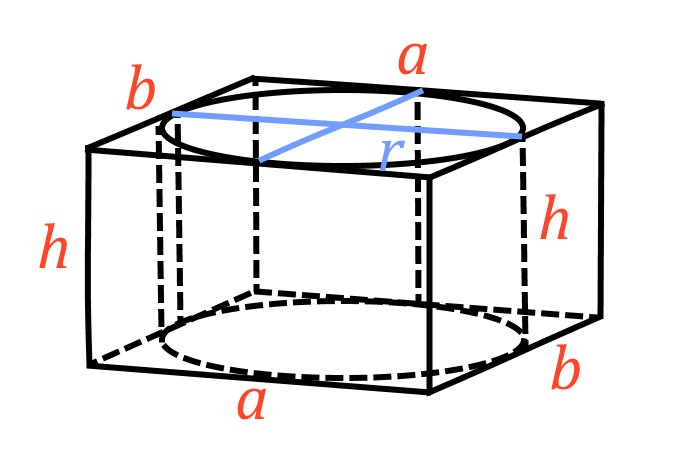
Действительно, или , откуда мы получаем, что .

Объем параллелепипеда, в основании которого лежит квадрат, определяется по формуле:

, где  — высота параллелепипеда и высота цилиндра (цилиндр вписан в параллелепипед),  — сторона основания.

Поскольку круг вписан в квадрат, значит, радиус круга будет равен , отсюда

Тогда формула объема параллелепипеда будет иметь вид:

,

откуда высота цилиндра

Подставляем данные:

,

Ответ:4