a) Решите уравнение ![]() .
.
б) Укажите корни этого уравнения, принадлежащие отрезку ![]() .
.
Решение.
a) Прежде чем решать данное уравнение, нам нужно упростить его: либо свести все к одной тригонометрической функции и к одному аргументы (или к ![]() или к
или к ![]() ), либо разложить на множители, произведение которых будет равно нулю.
), либо разложить на множители, произведение которых будет равно нулю.
Начнем применять известные нам формулы.
![]()
![]()
![]()
Применим эти формулы к нашему уравнению:
![]()
![]()
![]()
Вот мы и разложили левую часть на множители. И наше уравнение распадается на два простых уравнения.
Произведение двух множителей равно нулю, если или первый множитель равен нулю, или второй множитель равен нулю.
Получаем:
![]() или
или ![]()
Решим первое уравнение:
![]()
![]()
Посмотрим, где на тригонометрическом круге это значение и какой угол мы получаем:
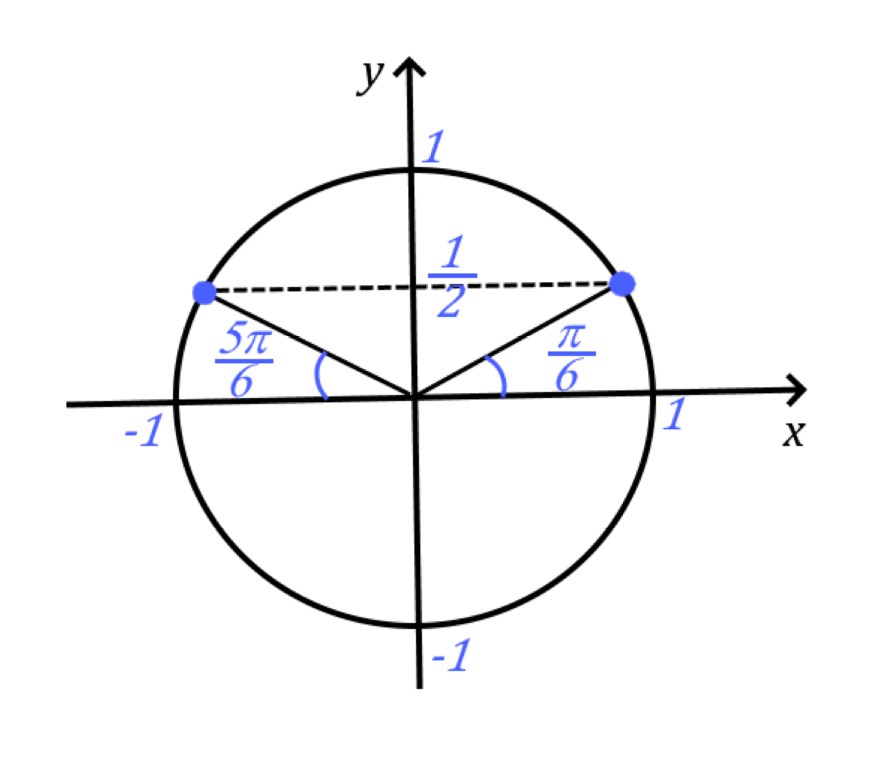
![]() , где
, где ![]() .
.
![]() , где
, где ![]() .
.
Решим второе уравнение:
![]()
![]() .
.
Решением этого уравнения будет ![]() , где
, где ![]() .
.
На тригонометрическом круге решение второго уравнения:
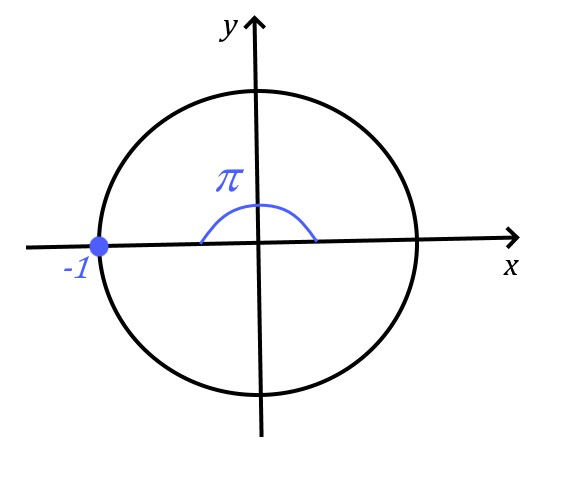
Ответ на пункт a) задания будет такой:
![]() , где
, где ![]() ,
,
![]() , где
, где ![]() ,
,
![]() , где
, где ![]() .
.
б) Найдем корни уравнения, которые принадлежат отрезку ![]() .
.
На помощь нам придет тригонометрический круг. Отметим на нем отрезок и нанесем корни, которые в него попали. Затем вычислим их значения.
Отрицательные углы на тригонометрическом круге откладываются по часовой стрелке. Начинаем двигаться от нуля — это единица на оси x и затем откладываем по часовой стрелке по четвертинке круга и считаем:
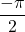 ,
,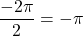 ,
,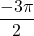 ,
,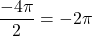 (замечаем эту точку и от нее начинаем отмечать отрезок),
(замечаем эту точку и от нее начинаем отмечать отрезок),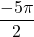 ,
,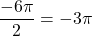 ,
,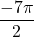 .
.
![Rendered by QuickLaTeX.com \displaystyle [-\frac{7\pi}{2}; -2\pi]](https://mathematics-repetition.com/wp-content/ql-cache/quicklatex.com-90eb06e867edc3dd04a87567145814db_l3.png)
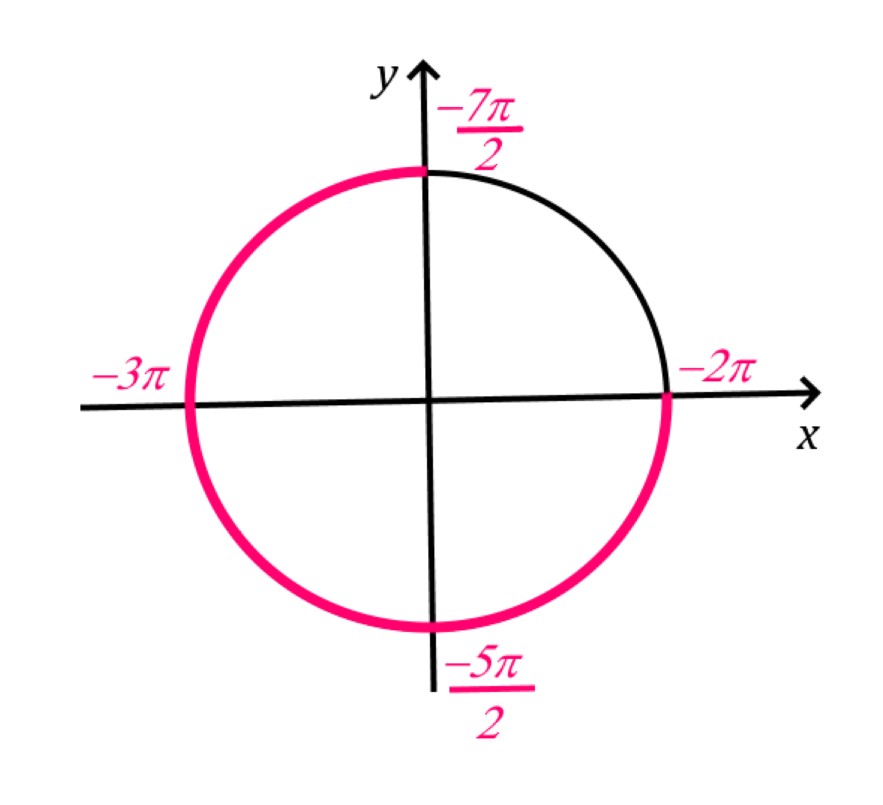
Теперь отметим на этом отрезке точки — корни уравнения, заметим, что корень ![]() в отрезок не вошел.
в отрезок не вошел.
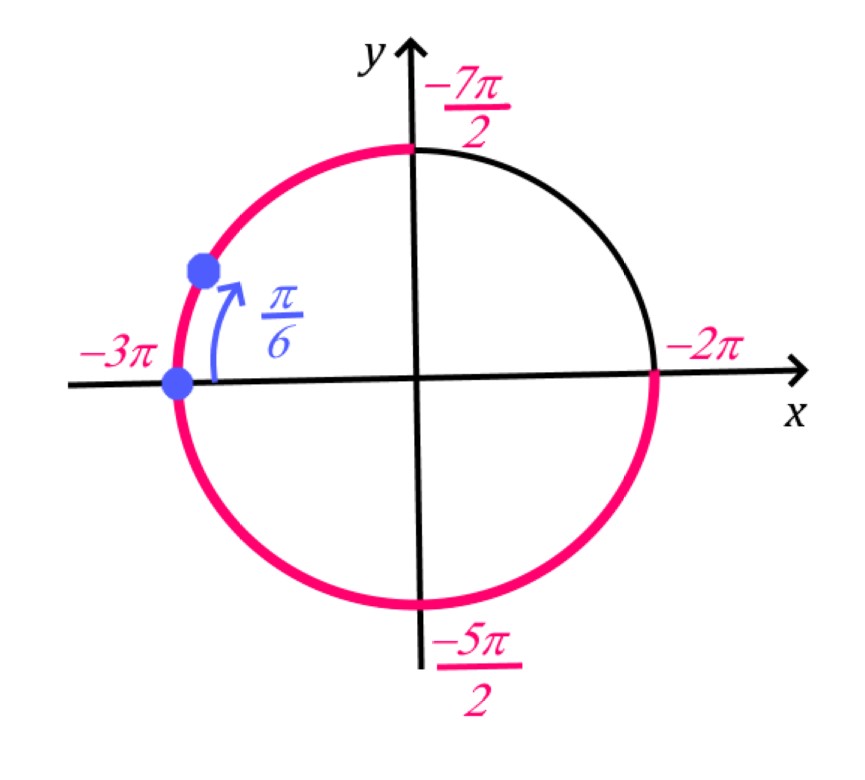
Если первый корень сразу виден: ![]() , то второй корень надо определить. Он расположен на расстоянии
, то второй корень надо определить. Он расположен на расстоянии ![]() от корня
от корня ![]() , если двигаться по часовой стрелке.
, если двигаться по часовой стрелке.
Тогда второй корень можно найти:
![]() .
.
Ответ на пункт б) будет: ![]() и
и ![]() .
.
Ответ: а)![]() , где
, где ![]() ,
, ![]() , где
, где ![]() ,
, ![]() , где
, где ![]() .
.
б) ![]() ;
; ![]() .
.

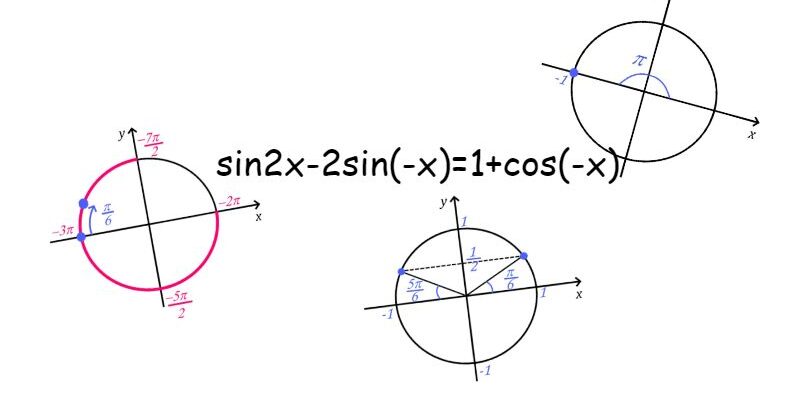








Сложная задача. Но все понятно. Я думал, что никогда не пойму как ее решать.