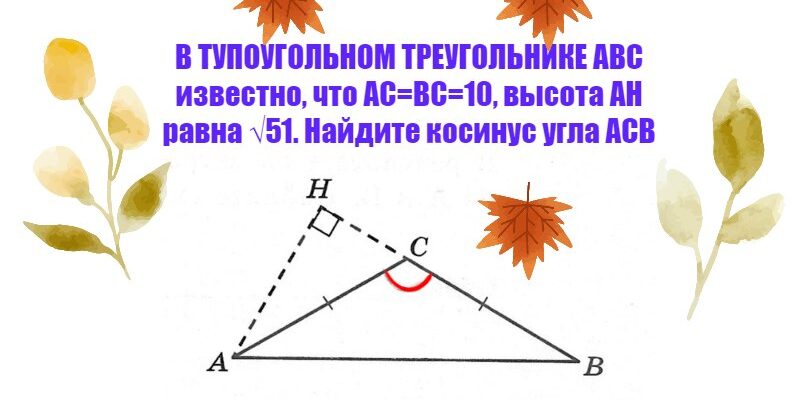
В тупоугольном треугольнике ABC известно, что AC=BC=10, высота AH равна √51

В тупоугольном треугольникеAbc известно что Ac=bc=10, высота Ah равна √51

ЕГЭ по математике профильный уровень

На чтение 1 мин. Просмотров 11k.

В тупоугольном треугольнике ABC известно, что AC=BC=10, высота AH равна √51. Найдите косинус угла ACB.

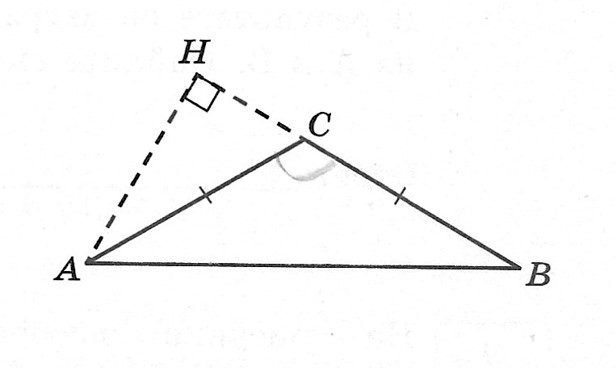
Решение:

Косинус угла ACB удобнее всего находить по теореме косинусов:

$AB^2=AC^2+CB^2-2 \cdot AC \cdot CB \cdot cos ABC$ .

Нам известны AC и CB, нужно лишь найти AB.

Для того, чтобы найти сторону AB из прямоугольного треугольника AHB, найдем сначала сторону HB.

$HB=HC+CB$ ,

CB известна по условию задачи. Найдем из треугольника AHC сторону HC по теореме Пифагора:

$HC^2=AC^2-AH^2$

$HC^2=100-51=49$

$HC=7$ .

Тогда $HB=17$

Теперь найдем AB: $AB^2=AH^2+HB^2=51+289=340$

Подставим значение AB в формулу теоремы косинуса: $AB^2=AC^2+CB^2-2 \cdot AC \cdot CB \cdot cos ABC$ ;

$340=100+100-2 \cdot 10 \cdot 10 cos ABC$ ;

$340=200-200 cos ABC$

$140=-200 cos ABC$

$cos ABC=\frac{140}{-200}=\frac{-7}{10}=-0,7$

Ответ: -0,7

геометрия в ЕГЭ геометрия треугольник задание 3 планиметрия

( 11 оценок, среднее 4.09 из 5 )

0 комментариев

Межтекстовые Отзывы

Посмотреть все комментарии