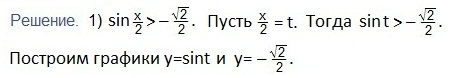На прошлом занятии «10.2.1. Решение тригонометрических неравенств. Часть 1» мы решили три неравенства вида sint < a. На этом уроке мы рассмотрим три неравенства вида sint > a, где -1≤а≤1.
Составим алгоритм решения.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=sint и y=a.
3. Находим такие две соседние точки пересечения графиков (поближе к оси Оу), между которыми синусоида располагается выше прямой у=а. Находим абсциссы этих точек.
4. Записываем двойное неравенство для аргумента t, учитывая период синуса (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Решаем первое неравенство
Построение графика синуса мы рассмотрели подробно в занятии «10.2.1. Решение тригонометрических неравенств. Часть 1».
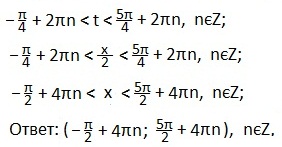Учитывая периодичность функции синуса, запишем двойное неравенство для значений аргумента t, удовлетворяющий последнему неравенству. Вернемся к первоначальной переменной. Преобразуем полученное двойное неравенство и выразим переменную х. Ответ запишем в виде промежутка.
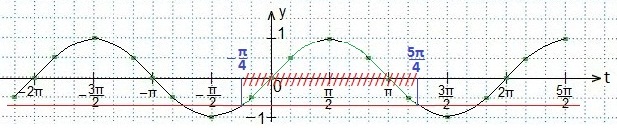
Решаем второе неравенство
При решении второго неравенства нам пришлось преобразовать левую часть данного неравенства по формуле синуса двойного аргумента, чтобы получить неравенство вида: sint≥a. Далее мы следовали алгоритму.
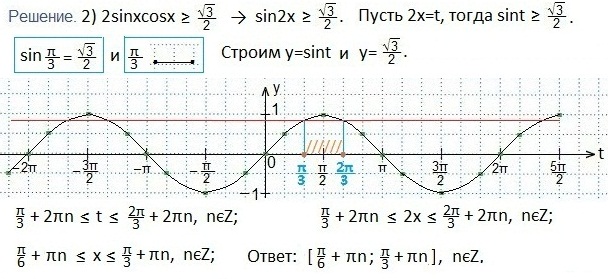
Решаем третье неравенство
Смотрите видео: «10.2.2. Решение тригонометрических неравенств. Часть 2.»
Дорогие выпускники и абитуриенты! Имейте ввиду, что такие способы решения тригонометрических неравенств, как приведенный выше графический способ и, наверняка, вам известный, способ решения с помощью единичной тригонометрической окружности (тригонометрического круга) применимы лишь на первых этапах изучения раздела тригонометрии «Решение тригонометрических уравнений и неравенств». Думаю, вы припомните, что и простейшие тригонометрические уравнения вы вначале решали с помощью графиков или круга. Однако, сейчас вам не придет в голову решать таким образом тригонометрические уравнения. А как вы их решаете? Правильно, по формулам. Вот и тригонометрические неравенства следует решать по формулам, тем более, на тестировании, когда дорога каждая минута. Итак, решите три неравенства этого урока по соответствующей формуле.
Если sint > a, где -1≤a≤1, то arcsin a + 2πn < t < π — arcsin a + 2πn, nєZ.
Учите формулы!
