На предыдущих занятиях мы решали тригонометрические неравенства следующих видов:
- sint < a (10.2.1. Решение тригонометрических неравенств. Часть 1.)
- sint > a (10.2.2. Решение тригонометрических неравенств. Часть 2.)
- cost < a (10.2.3. Решение тригонометрических неравенств. Часть 3.)
- cost > a (10.2.4. Решение тригонометрических неравенств. Часть 4.)
- tgt < a (10.2.5. Решение тригонометрических неравенств. Часть 5.)
На этом занятии мы будем решать неравенства вида tgt > a.
Будем применять следующий алгоритм решения (как на прошлом уроке):
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=tgt и y=a.
3. Находим промежуток значений t, при которых тангенсоида располагается выше прямой у=а. Левая граница этого промежутка arctg a, а правая всегда (π/2)
4. Записываем двойное неравенство для аргумента t, учитывая наименьший период тангенса Т=π (t будет между абсциссами arctg a и (π/2) ).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Первое неравенство
Решение.
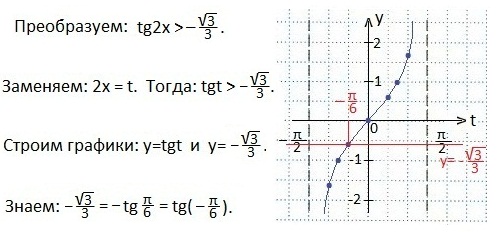
Разделим обе части неравенства на 3. Сделаем замену данной переменной на t. Тогда получим более простое неравенство.
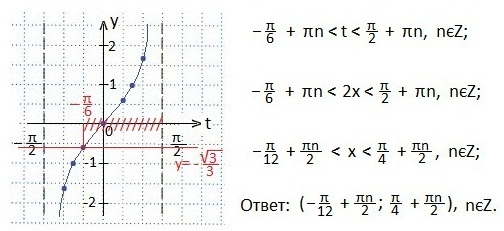
Определим промежуток значений переменной t, при которых неравенство будет верным. Это абсциссы тех точек графика функции y=tg t, которые лежат выше нашей прямой. Покажем штриховкой эти значения t. Запишем найденные значения аргумента t в виде двойного неравенства.
Второе неравенство
Решение.
Преобразуем левую часть неравенства по формуле tg (α+β) и получим более простое неравенство. Делаем замену переменной.
Определяем искомый промежуток значений переменной t. Затем выразим х и запишем ответ в виде промежутка. Учтем, что неравенство нестрогое, но что тангенса (π/2) не существует.
Третье неравенство
Решение.
Применяем правило для формул приведения:
1) перед приведенной функцией ставят знак приводимой; 2) если в записи аргумента (π/2) взято нечетное число раз, то функцию меняют на кофункцию.
Наш аргумент находится в 3-ей четверти, а котангенс в 3-ей четверти имеет знак «плюс», поэтому, знак приведенной функции не поменяется. В записи данного аргумента (π/2) взято 3 раза (нечетное число), поэтому функцию котангенс поменяем на кофункцию — тангенс.
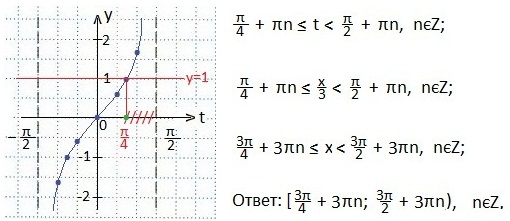
Теперь данное неравенство приняло вид: tgt≥1. Построим графики функций y=tgt и у=1. Определим промежуток значений аргумента t, при которых неравенство tgt≥1 будет верным. Ответ запишем в виде промежутка. Неравенство у нас нестрогое, но правый конец промежутка не входит в решение неравенства, так как тангенса (π/2) не существует.
Подробные решения этих неравенств смотрите в видео: «10.2.6. Решение тригонометрических неравенств. Часть 6.»
Дорогие друзья! Мы решили неравенства с тангенсом графическим способом, но, конечно, существует и более короткое решение — по формулам.
Если tgt < a, то (- π/2) + πn < t < arctg a + πn, где nєZ.
Если tgt > a, то arctg a + πn < t < (π/2) + πn, где nєZ.
Выучите эти формулы, и вы будете решать тригонометрические неравенства с тангенсом быстрее!
