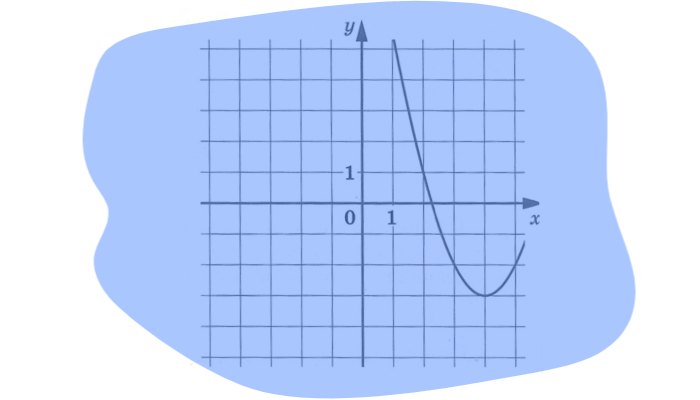
На рисунке изображен график функции f(x)=ax^2+bx+c, где a, b и c

На рисунке изображен график функции f (x)=ax^2+bx+c где a, b и c — целые. Найдите f (-5)

На чтение 2 мин. Просмотров 89.8k.

На рисунке изображен график функции $f(x)=ax^2+bx+c$ , где $a$ , $b$ и $c$ — целые. Найдите $f(-5)$ .

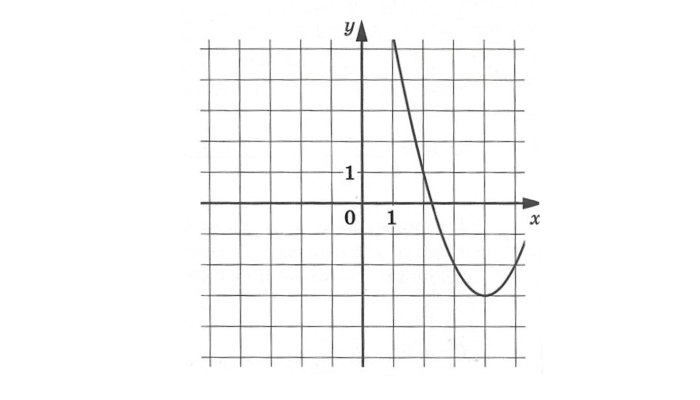
Решение:

Графиком функции является парабола. Чтобы найти три неизвестных нам нужно составить три уравнения для этих неизвестных. Два из них можно взять из формул для координат вершины параболы и одно, если известны координаты любой точки параболы. Вершина параболы находится в точке $(4;-3)$ .

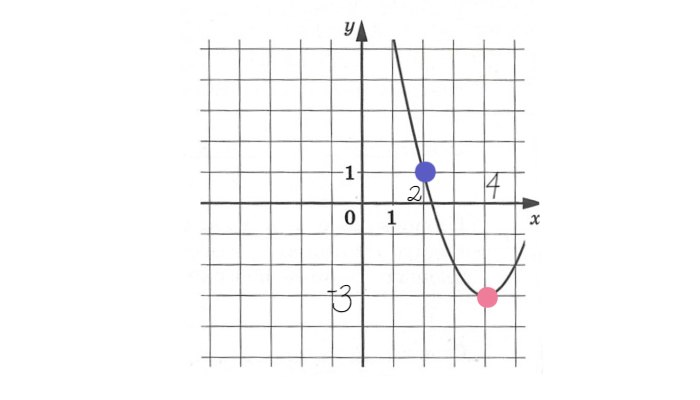
Известно, что координаты вершины параболы находятся по формулам:

$m=\frac{-b}{2a}$ — координата $x$ вершины параболы.

$n=\frac{4ac-b^2}{4a}$ — координата $y$ вершины параболы.

Кроме того, нам известны координаты еще трех точек параболы, возьмем любую из них. Например, точку с координатами $(2;1)$ .

Получаем три уравнения:

$4=\frac{-b}{2a}$

$-3=\frac{4ac-b^2}{4a}$

$1=a \cdot 2^2+b\cdot 2+c$

Получаем систему уравнений.

$\left\{ \begin{aligned} 4=\frac{-b}{2a}, \\ -3=\frac{4ac-b^2}{4a}, \\ 1=a \cdot 2^2+b\cdot 2+c. \end{aligned} \right.$

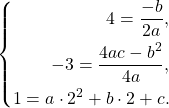
Из первого уравнения системы находим связь между $a$ и $b$ :

$8a=-b$ ,

$b=-8a$ .

Тогда мы можем записать остальные два уравнения системы так:

$\left\{ \begin{aligned} b=-8a, \\ -3=\frac{4ac-64a^2}{4a}, \\ 1=a \cdot 2^2-8a\cdot 2+c. \end{aligned} \right.$

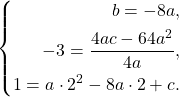
Из второго уравнения системы можно получить:

$-3=\frac{4c-64a}{4}$ или $-3=c-16a$ , тогда $c=16a-3$ . Подставим в третье уравнение системы вместо $c$ :

$1=a \cdot 2^2+(-8a) \cdot 2+16a-3$

Упростим:

$1=4a-16a+16a-3$

$a=1$ ,

тогда $b=-8a=-8$ и $c=16-3=13$ .

Искомое уравнение параболы будет иметь вид: $f(x)=x^2-8x+13$ .

Теперь определим то, что у нас спрашивают — $f(-5)$ :

$f(-5)=(-5)^2-8 \cdot (-5) +13=25+40+13=78$ .

Ответ: 78

Замечание

Решить задачу можно намного проще, если учесть, что коэффициент $a$ отвечает за «ширину» параболы. Если не обращать внимания на то, что вершина параболы не находится в точке — начале координат, то видно, что это парабола $y=x^2$ . Просто наша парабола смещена относительно оси $Ox$ и относительно оси $Oy$ . В дальнейшем, сравнивая параболу с известными вам параболами $y=x^2$ , $y=2x^2$ , мы можем сразу определить коэффициент $a$ . В этом задании он равен 1.