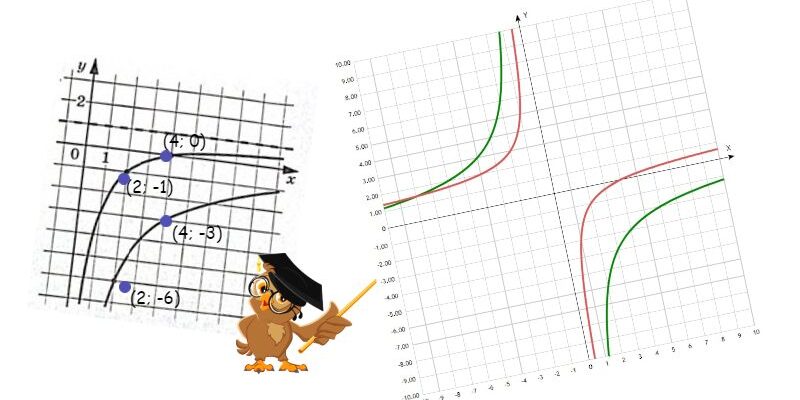
На рисунке изображены части графиков функций 
и 
. Найдите абсциссу точки пересечения графиков этих функций.
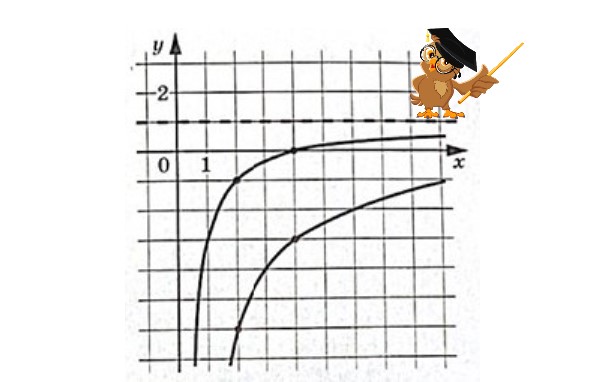
Решение.
Для точного определения функции, необходимо знать значения коэффициентов 
, 
и 
. Для того, чтобы их найти, возьмем известные точки на данном нам графике.
График 
расположен ниже графика так как он не смещен в вертикальном направлении и не пересекает ось 
, у него отсутствует коэффициент (свободный член) смещения.
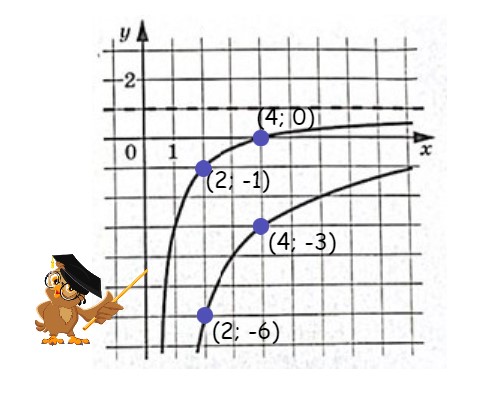
Для него возьмем точки с координатами 
и 
. Эти точки отмечены на графике, хотя для первой функции нам достаточно взять координаты одной точки.
Совет. Не берите никаких других точек, даже если вам кажется, что их координаты заданы точно (например, они пересекают линии масштаба). Те точки, координаты которых вы можете взять уже отмечены на графике.
Определим для первой функции , подставив в нее координаты точки .
Получим:
.
Отсюда находим, что 
.
Проверим, используя координаты второй точки:
.
Итак, первая функция определена: 
.
Определим вид второй функции. В ней две неизвестных, поэтому необходимо решить систему из двух уравнений, каждое из которых получается, если в исходное уравнение 
подставить координаты точки.
На графике находим координаты двух точек: 
и 
.
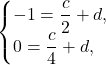
Из первого уравнения системы выразим через .
.
Подставим это выражение во второе уравнение системы:
.
Упростим и найдем :
.
Определим .
Решение системы:
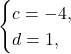
Итак, вторая функция будет иметь вид: 
.
Нам в задаче нужно найти абсциссу точки пересечения графиков двух функций. То есть найти координату 
точки пересечения.
Если графики пересекаются, то в точке пересечения равны и абсциссы (
) и ординаты (
).
Если левые стороны уравнений функций равны, то равны и правые:
Решим полученное уравнение:
.
Сделаем проверку. Подставим значение сначала в первое уравнение, потом во второе уравнение. Значения 
и 
должны совпасть.
.
.
Задача решена верно.
Посмотрите, если построить графики этих функций, то вот где будет точка их пересечения.
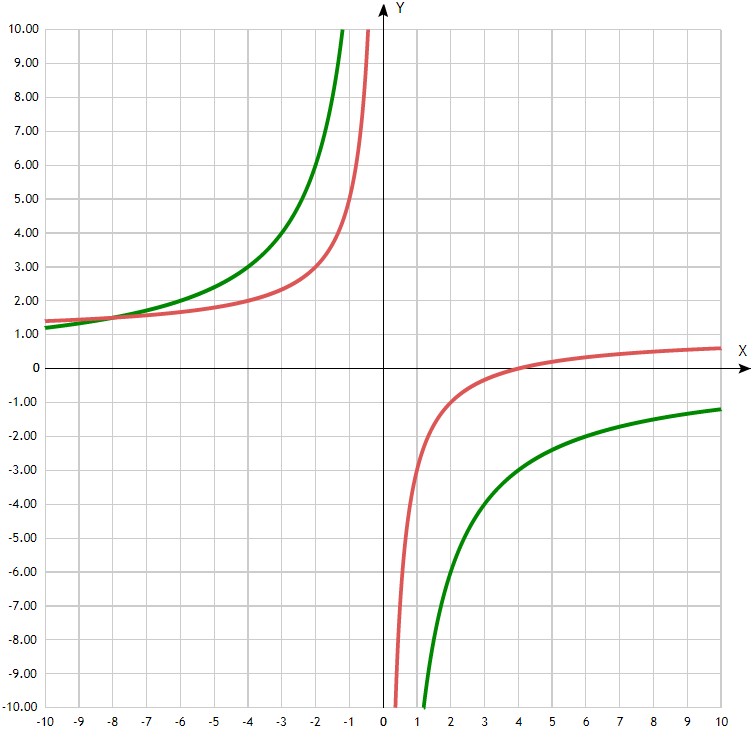
Ответ: 
.
Похожая задача решена здесь.
