На рисунке изображён график функции f(x)=ax^2+bx+c. Найдите c.

На рисунке изображён график функции f (x)=ax^2+bx+c. Найдите c

На чтение 2 мин. Просмотров 20k.

На рисунке изображён график функции f (x)=ax^2+bx+c. Найдите c.

Рисунок к задаче 10 на рисунке изображен график функции — Рисунок к задаче. На рисунке изображен график функции f (x)

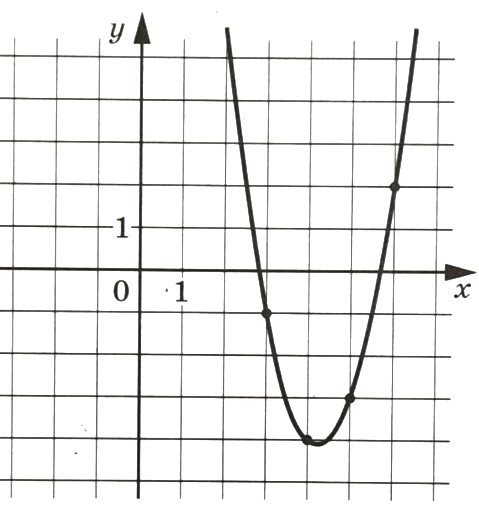
Решение:

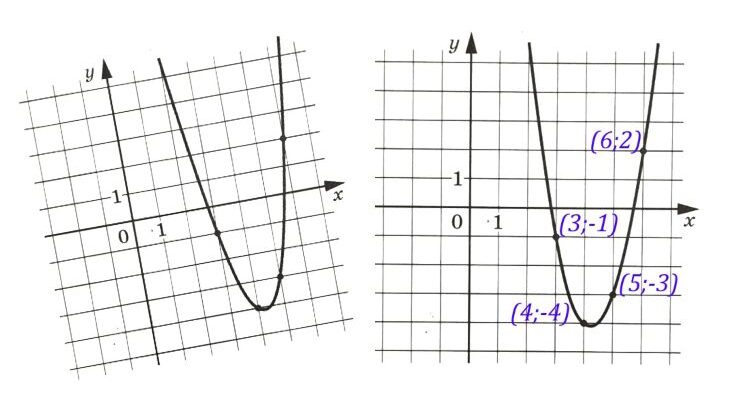
Нам даны точные координаты четырех точек — они отмечены на рисунке точками. Это точки с координатами (3; -1), (4; -4), (5; -3), (6; 2).

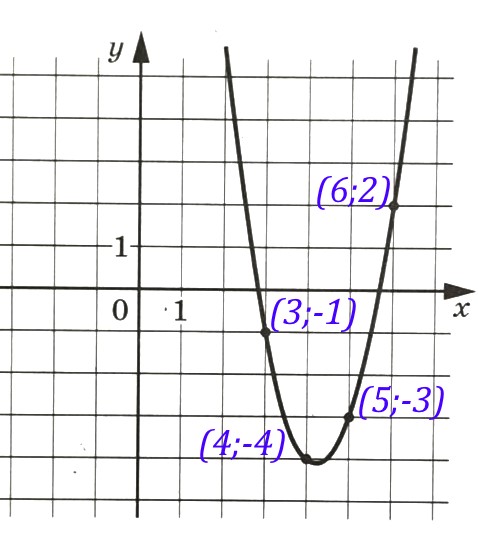
В уравнении $f (x)=ax^2+bx+c$ три неизвестных, значит, нам достаточно взять три точки и подставить их координаты в уравнение функции, а затем решить полученную систему из трех уравнений с тремя неизвестными.

Итак, получим:

$\begin{cases} 9a+3b+c=-1 (1), \\ 16a+4b+c=-4 (2), \\ 25a+5b+c=-3 (3). \end{cases}$

От второго уравнения системы отнимем первое уравнение:

$16a-9a+4b-3b+c-c=-4- (-1)$
$7a+b=-3$

Теперь отнимем от (3) -го (2) -е уравнение, получим:

$25a-16a+5b-4b+c-c=-3- (-4)$
$9a+b=1$

И нашу систему можно записать в виде:

$\begin{cases} 9a+3b+c=-1, \\ 7a+b=-3, \\ 9a+b=1. \end{cases}$

Теперь из (3) вычтем (2):

$9a-7a+b-b=1- (-3)$
$2a=4$
$a=2$

Найдем $b$ из равенства: $9a+b=1$ ; $b=1-9a=1-18=-17$

Полученные значения $a$ и $b$ подставим в (1):

$9a+3b+c=-1$
$9 \cdot 2+3 \cdot (-17)+c=-1$
$18-51+c=-1$
$c=-1+51-18$
$c=50-18$
$c=32$

Уравнение функции тогда $f (x)=2x^2-17x+32$

Проверим правильность найденной функции, подставив в полученное уравнение координаты четвертой точки (6; 2), которые мы не использовали для составления системы уравнений:

$2=2 (6)^2-17 \cdot 6+32$
$2=72-102+32$
$2=-30+32$
$2=2$

Все верно. Таким образом, значение с=32.

Ответ: 32.