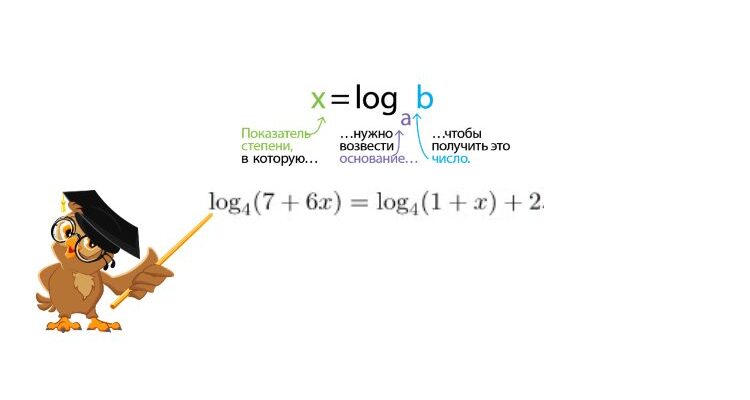
Найдите корень уравнения log4 (7+6x)=log4 (1+x)+2

Найдите корень уравнения Log4(7+6x)=log4(1+x)+2

ЕГЭ по математике профильный уровень

На чтение 1 мин. Просмотров 3.8k.

Найти корень логарифмического уравнения непросто - сначала, возможно, потребуется упрощение уравнения, применение известных свойств логарифма. Цель - сделать так, чтобы и слева, и справа от равенства был логарифм по одинаковому основанию.

Найдите корень уравнения $\log_4(7+6x)=\log_4(1+x)+2$ .

Решение:

Представим 2 в виде логарифма, используя свойство $a=a \log_m m=\log_m m^a$ , где $m$ -любое положительное число ( $m \neq 1$ ) и $\log_m m=1$ .

Получим:

$2=\log_4 4^2$ .

Уравнение примет вид:

$\log_4(7+6x)=\log_4(1+x)+\log_4 4^2$

$\log_4 (7+6x)=\log_4 (1+x)\cdot 16$

Здесь мы упростили $\log_4(1+x)+\log_4 4^2$ , использовав свойство логарифмов: $\log_a b+\log_a c=\log_a bc$

Слева логарифм по основанию 4 и справа логарифм по основанию 4, значит, будут равны и числа под знаком логарифма:

$7+6x=16(1+x)$

Решим полученное уравнение:

$7+6x=16+16x$

$-10x=9$

$x=-0,9$ .

Так как число под знаком логарифма не может быть отрицательным, проверим $7+6x>0$ и $1+x>0$ .

$7+6(-0,9)=1,6>0$

$1-0,9=0,1>0$

Проверка:

$\log_4(7+6(-0,9))=\log_4(1-0,9)+2$

$\log_4 1,6=\log_4 0,1 +\log_4 16$

$\log_4 1,6=\log_4 1,6$

Уравнение решено верно.

Ответ: -0,9.

( 3 оценки, среднее 5 из 5 )

1 Комментарий

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии

Семён

Спасибо! Есть не только решение задачи, но и понятно теперь, как решать другие такие же. Очень полезно!!!

0

Ответить