Найдите значение выражения ![]()
Для решения подобных заданий нужно будет вспомнить формулы приведения тригонометрических функций. Посмотреть их можно здесь: формулы приведения, или вы можете использовать простое правило приведения.
Решение:
Нам нужно привести и в числителе и в знаменателе синус одного угла, чтобы мы их могли сократить и осталось бы числовое значение, которое мы и запишем в ответ.
Из ![]() можно получить
можно получить ![]() , если представить: 299º=360º-61º и использовать правило приведения тригонометрических функций.
, если представить: 299º=360º-61º и использовать правило приведения тригонометрических функций.
Тогда получим: ![]() .
.
![]() можно привести по формулам приведения.
можно привести по формулам приведения. ![]()
Или воспользоваться правилом приведения: если в аргументе приводимой функции можно выделить число, кратное ![]() , где
, где ![]() — целое число (то есть выделяется целое число
— целое число (то есть выделяется целое число ![]() ), то функция остается прежней и ставится знак приводимой функции. У нас уже выделено число 360º=2
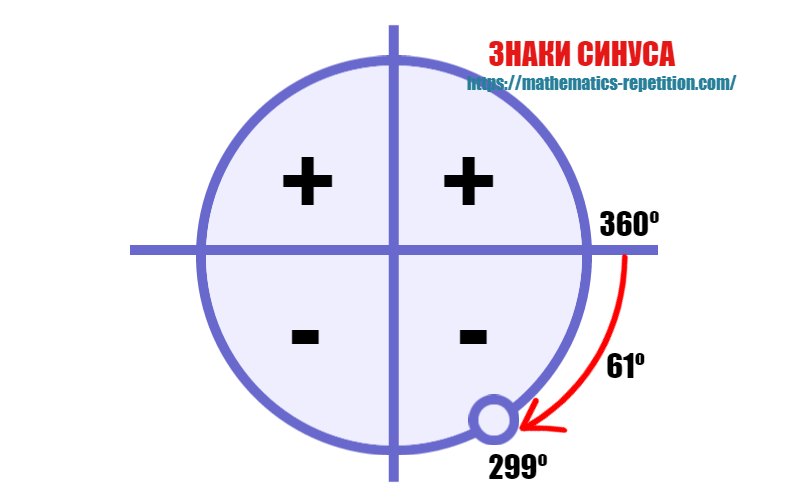
), то функция остается прежней и ставится знак приводимой функции. У нас уже выделено число 360º=2![]() , то у нас синус остается синусом. Теперь разберемся со знаком. Посмотрим в какую четверть попадает аргумент 360º-61º. Это четвертая четверть. В этой четверть синус отрицательный. Поэтому и получается, что
, то у нас синус остается синусом. Теперь разберемся со знаком. Посмотрим в какую четверть попадает аргумент 360º-61º. Это четвертая четверть. В этой четверть синус отрицательный. Поэтому и получается, что ![]() .
.
Подставим найденное значение синуса по правилу приведения в нашу исходную дробь:
![]()
Ответ: -5









