Матрица содержит в себе векторы-столбцы. Они по-разному ориентированы в пространстве. Характеристикой этого расположения и того матричного преобразования, которое может дать матрица, выступает определитель матрицы.
Содержание
Определитель матрицы 2×2
Пусть дана квадратная матрица второго порядка:
A=\begin{pmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{pmatrix}
Определителем (или детерминантом) второго порядка, соответствующим данной матрице, называется число a_{11}a_{22}-a_{12}a_{21}.
Определитель второго порядка записывается так:
detA=\begin{vmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}
Геометрический смысл определителя
Если нам дана квадратная матрица
A=\begin{pmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{pmatrix}
То первый столбец дает нам координаты одного вектора, а второй столбец чисел — координаты второго вектора. Начало данных векторов — в точке начала координат.
Тогда определитель матрица дает нам площадь параллелограмма, построенного на данных векторах.
Рассмотрим на примере
Пусть нам дана матрица с координатами:
A=\begin{pmatrix} 3& 1\\ 1& 2 \end{pmatrix}
Нарисуем координатную плоскость и отметим на ней данные векторы.
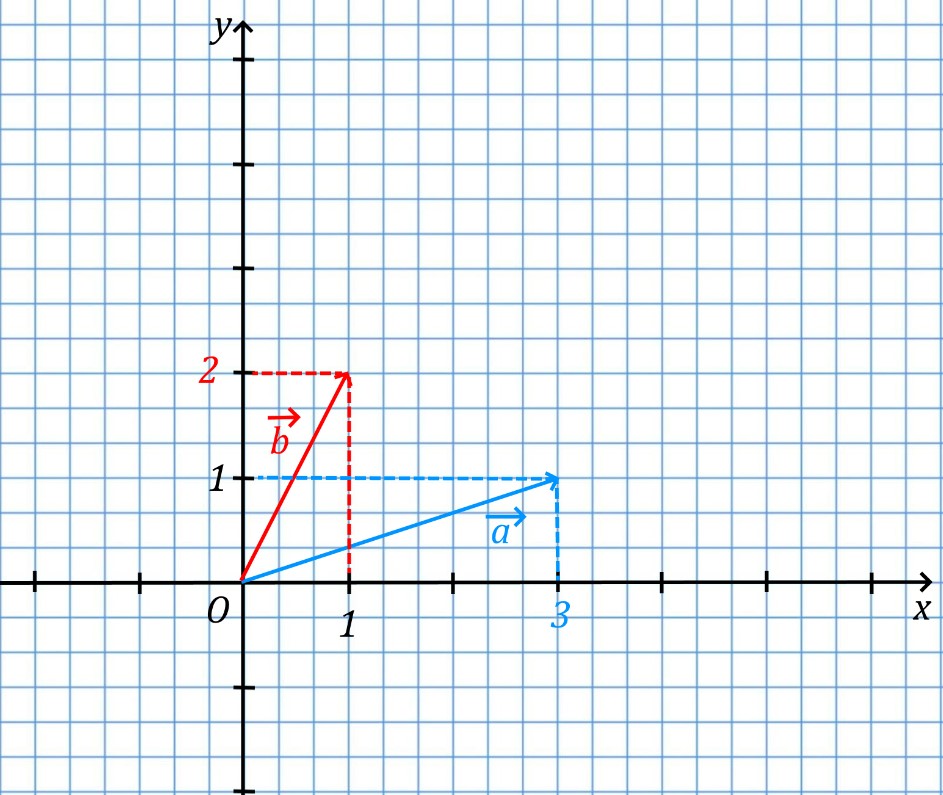
и 
Где у вектора \overline{a} координаты (3; 1), а у вектора \overline{b} координаты (2; 1).
Теперь построим на этих векторах параллелограмм, считая, что векторы a и b его стороны. Получим:
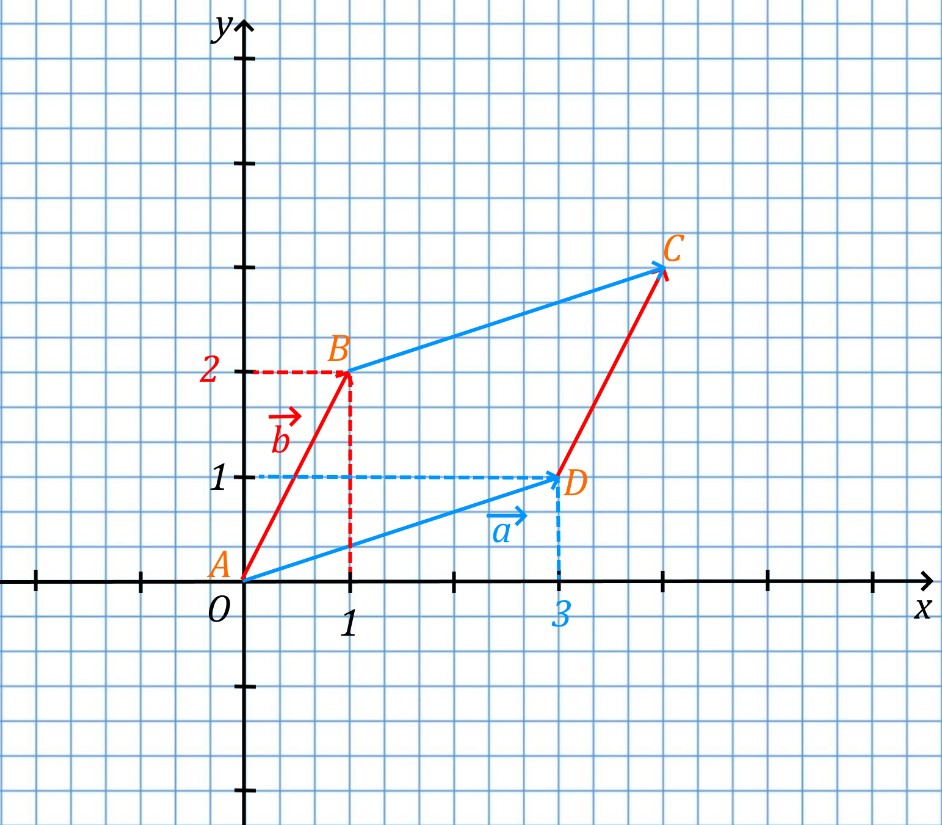
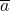и
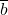
Площадь данного параллелограмма и будет являться определителем матрицы. Площадь данного параллелограмма S_{ABCD}=5. И определитель матрицы:
detA=\begin{vmatrix} 3& 1\\ 1& 2 \end{vmatrix}=3 \cdot 2-1 \cdot 1=6-1=5
Однако, обычно в линейной алгебре говорят не о площади параллелограмма, а о матричном преобразовании. То есть о том, в какую фигуру матрица преобразует единичный квадрат, построенный на единичных векторах. Насколько она ее масштабирует в пространстве. То есть вот из такого квадрата (синий цвет) матричное преобразование делает параллелограмм с определенной площадью (отмечено красным цветом), равной по модулю определителю матрицы.
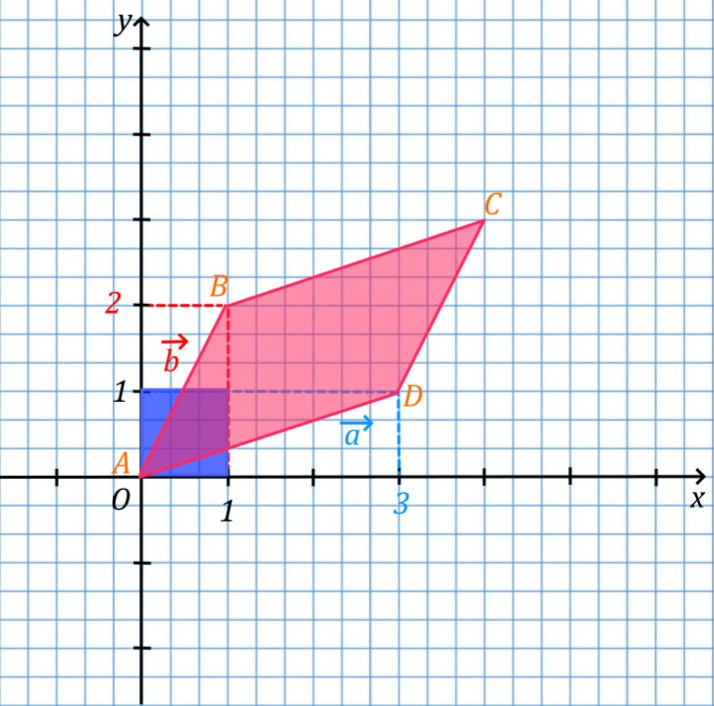
Однако иногда определитель матрицы может быть отрицательным числом. В этом случае площадь фигуры, построенной на векторах матрицы, будет равна модулю данного числа, а знак минус означает, что ориентация данной фигуры отрицательна.
Можно расширить геометрический смысл матрицы и на матрицы другого размера.
Таким образом, определитель матрицы 1×1 дает длину вектора, 2×2 — площадь параллелограмма, 3×3 — объем параллелепипеда, а nxn — объем n-мерного параллелепипеда.
Примеры на вычисление определителя второго порядка
Вычислить определители:
a) \begin{vmatrix} 4& 7\\ 2& 6 \end{vmatrix}
Решение:
\begin{vmatrix} 4& 7\\ 2& 6 \end{vmatrix}=4 \cdot 6-7 \cdot 2=24-14=10
Ответ: 10
б) \begin{vmatrix} m^2& nm\\ nm& n^2 \end{vmatrix}
Решение:
\begin{vmatrix} m^2& nm\\ nm& n^2 \end{vmatrix}=m^2 \cdot n^2-nm \cdot nm=m^2n^2-n^2m^2=0
Ответ: 0
Определитель третьего порядка
Пусть дана квадратная матрица третьего порядка:
A=\begin{pmatrix} a_{11}& a_{12} & a_{13}\\ a_{21}& a_{22} & a_{23} \\ a_{31}& a_{32} & a_{33} \end{pmatrix}
Определителем (или детерминантом) третьего порядка, соответствующим данной матрице, называется число:
a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{33}a_{21}-a_{11}a_{23}a_{32}
Определитель третьего порядка будет:
detA=\begin{vmatrix} a_{11}& a_{12} & a_{13}\\ a_{21}& a_{22} & a_{23} \\ a_{31}& a_{32} & a_{33}\end{vmatrix}= \\ =a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{33}a_{21}-a_{11}a_{23}a_{32}
Правило треугольников
При вычислении определителей третьего порядка удобно пользоваться правилом треугольников (правилом Саррюса). Это правило проиллюстрируем на схеме:
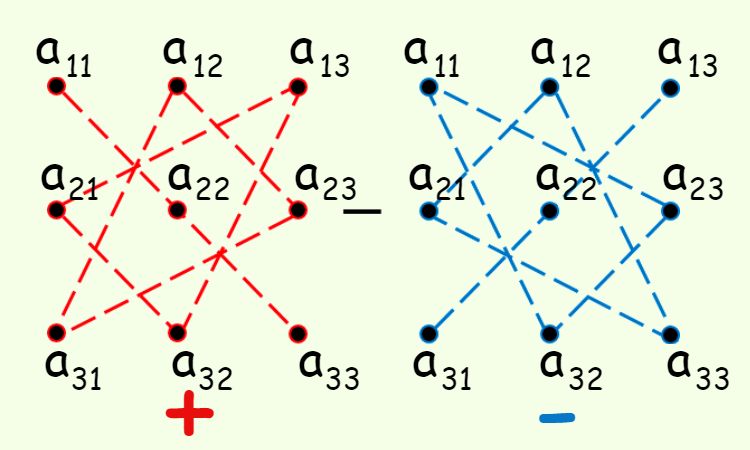
Как пользоваться правилом треугольника:
На схеме есть две картинки — красная и синяя, красная картинка дает нам три положительных слагаемых в формуле определителя третьего порядка, а синяя — три отрицательных.
Умножаем так — сначала умножаем элементы матрицы по главной диагонали 
потом в вершинах одного треугольника 
и в вершинах другого треугольника: 
. Все полученные множители складываем.
Теперь обратимся к синей картинке. Тут мы начинаем сначала перемножать элементы по побочной диагонали: 
, а потом элементы в вершинах двух треугольников: 
и 
. Полученные множители записываем в формулу со знаком минус.
Примеры на вычисление определителя третьего порядка
a) Вычислить определитель матрицы:
A=\begin{pmatrix} 2& 3 & 4\\ 6& 5 & 7 \\ 9& 0& 8 \end{pmatrix}
Решение:
det A=\begin{vmatrix} 2& 3 & 4\\ 6& 5 & 7 \\ 9& 0 & 8 \end{vmatrix}=2 \cdot 5 \cdot 8+ 3 \cdot 7 \cdot 9+6\cdot 0 \cdot 4 — 4 \cdot 5 \cdot 9 — 3 \cdot 6 \cdot 8 — 7 \cdot 0 \cdot 2=80+189+0-180-144-0=-55
Ответ: det A=-55
б) Вычислить определитель матрицы 3×3:
A=\begin{pmatrix} 2& 3 & 1\\ 1& -5 & 6\\ 2& -3& 4 \end{pmatrix}
Решение:
Используем формулу определителя третьего порядка
det B=\begin{vmatrix} 2& 3 & 1\\ 1& -5 & 6\\ 2& -3& 4 \end{vmatrix}=2 \cdot (-5) \cdot 4+ 3 \cdot 6 \cdot 2+1\cdot 1 \cdot (-3) — 1 \cdot (-5) \cdot 2 — 2 \cdot 6 \cdot (-3) — 3 \cdot 1 \cdot 4=-40+36-3+10+36-12=27
Ответ: det B=27
в) Вычислите определитель единичной матрицы 3×3.
Решение:
Единичная матрица 3×3 имеет вид:
A=\begin{pmatrix} 1& 1 & 1\\ 1& 1 & 1\\ 1& 1& 1 \end{pmatrix}
Используем формулу определителя третьего порядка
det A=\begin{vmatrix} 1& 1 & 1\\ 1& 1 & 1\\ 1& 1& 1 \end{vmatrix}=1 \cdot 1 \cdot 1+ 1 \cdot 1 \cdot 1+1\cdot 1 \cdot 1 — 1 \cdot 1 \cdot 1 — 1 \cdot 1 \cdot 1 — 1 \cdot 1 \cdot 1=1+1+1-1-1-1=0
Действительно, в столбцах единичной матрицы три совпадающих вектора, на которых невозможно построить объемную фигуру, объем которой и определяет определитель матрицы третьего порядка. Поэтому мы и получили число 0.
Вообще говоря, любая матрица с одинаковыми строками и столбцами дает определитель, равный нулю. Можете проверить самостоятельно.
Ответ: 0
Разложение определителя по строке или столбцу, а также его свойства, миноры и дополнения элементов определителя рассмотрим далее.
Спасибо, помогли с примером.