Рассмотрим в данной статье такие линейные операции над матрицами — сложение матриц. Дадим определение суммы матриц и приведем примеры на сложение матриц с подробным объяснением. Приведем свойства сложения матриц
Содержание
Сложение матриц
Сумма матриц A и B — это матрица C, в которой все элементы есть суммы соответствующих элементов матриц A и B. При этом сами матрицы должны иметь одинаковое строение — или быть прямоугольными типа
, либо квадратными.
Итак, пусть нам даны матрицы
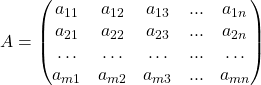
и
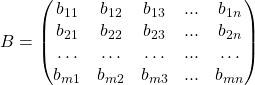
Тогда сумма матриц ![]() :
:
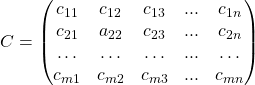
где ![]() ,
, ![]() ,
, ![]() , ... ,
, ... , ![]() ,
, ![]() , ...,
, ..., ![]() , ...,
, ..., ![]() .
.
Примеры сложения матриц
Пример 1
Сложите матрицы A и B, если:
![]()
и
![]()
Решение:
Матрицы A и B имеют одинаковое строение, значит мы можем их сложить, получим матрицу С:
![]()
Пример 2
Сложить матрицы A и B, если:
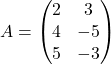
и
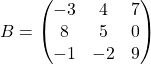
Решение:
Матрицы A и B сложить нельзя, так как матрица A — это матрица ![]() , а матрица B — это матрица
, а матрица B — это матрица ![]() , а мы можем складывать только прямоугольные матрицы одного порядка.
, а мы можем складывать только прямоугольные матрицы одного порядка.
Пример 3
Сложить матрицы A и B, если:
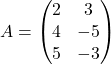
и
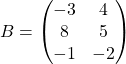
Решение: матрицы имеют одинаковое прямоугольное строение, значит, их можно сложить:
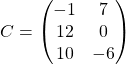
Свойства сложения матриц
Так как при сложении матриц мы в основном складываем числа, то и свойства сложения чисел распространяются и на сложение матриц:
- Переместительный закон сложения:
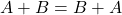 , где
, где  и
и  либо квадратные матрицы одного порядка
либо квадратные матрицы одного порядка 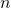 , либо прямоугольные матрицы одного типа
, либо прямоугольные матрицы одного типа 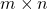 .
. - Сочетательный закон сложения
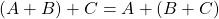 , где
, где 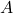 ,
, 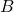 и
и 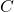 — либо квадратные матрицы одного порядка
— либо квадратные матрицы одного порядка 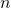 , либо это матрицы прямоугольные размерностью
, либо это матрицы прямоугольные размерностью 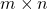 .
. - Сумма матрицы и нулевой матрицы равна исходной матрице:
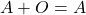 .
. - Сумма матрицы и противоположной матрицы равна нулевой матрице:
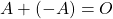 .
.
Противоположная матрица
Не путайте противоположную матрицу с обратной матрицей. Это разные матрицы.
Например, давайте найдем матрицу ![]() , противоположную матрице
, противоположную матрице ![]() :
:
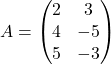 ,
,
Очевидно, что это будет матрица:
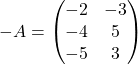
Соответственно при сложении матриц ![]() мы получим нулевую матрицу:
мы получим нулевую матрицу:
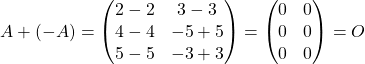
Вычитание матриц
Так как любое вычитание можно заменить сложением, то вычитание матриц можно заменить сложением матриц, например, вычитание из матрицы A матрицы B:
это есть сложение матрицы A и матрицы, противоположной матрице B:
.

Рассмотрим на примере: пусть нам нужно вычислить разность матриц
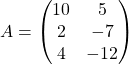
и
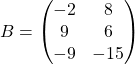
Находим разность этих матриц, как сложение матрицы A и матрицы, противоположной матрице B:
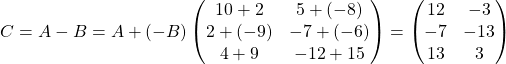
На примере видно, что разность двух матриц — это матрица, элементы которой получены путем вычитания из соответствующих элементов первой матрицы соответствующих элементов второй матрицы.
Посмотрите еще статьи про матрицы:







